【抽象代数】Mathematica怎么分析s4

1、列举S4的所有元素：S4 = GroupElements[SymmetricGroup[4]]这个群有24个元素。

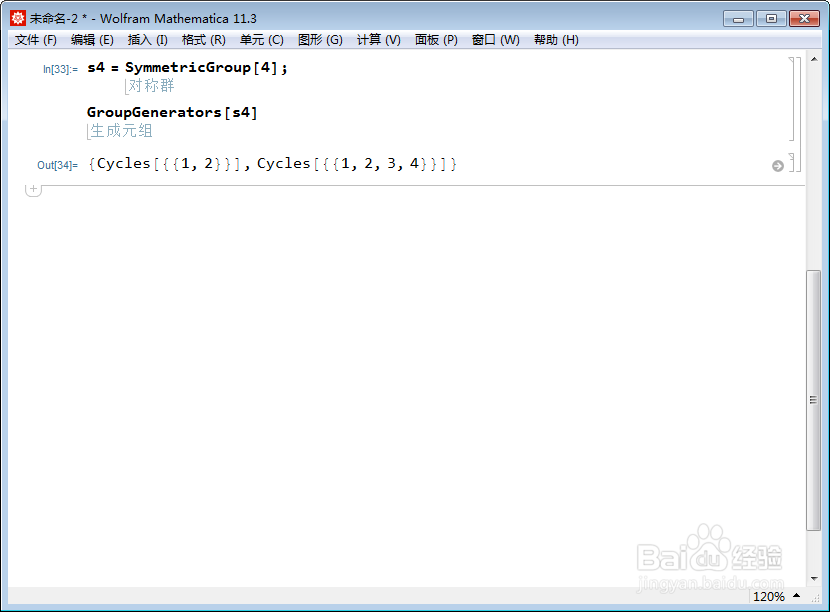
2、求出这个群的最小生成元集合：s4 = SymmetricGroup[4];GroupGenerators[s4]

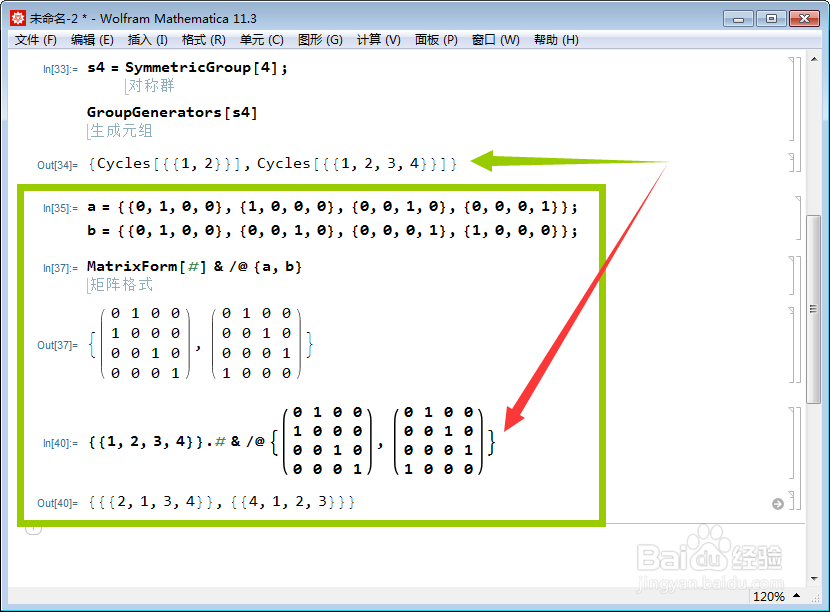
3、给出生成元的矩阵表示：a = {{0, 1, 0, 0}, {1, 0, 0, 0}, {0, 0荑樊综鲶, 1, 0}, {0, 0, 0, 1}};b = {{0, 1, 0, 0}, {0, 0, 1, 0}, {0, 0, 0, 1}, {1, 0, 0, 0}};容易验证，a可以代表Cycles[{{1, 2}}]，{{1,2,3,4}}与矩阵a的乘积，表示把第一个元素和第二个元素轮换位置，其余位置的元素不变；b可以代表Cycles[{{1, 2, 3, 4}}]，{{1,2,3,4}}与矩阵b的乘积，表示四个元素轮换一个位置。

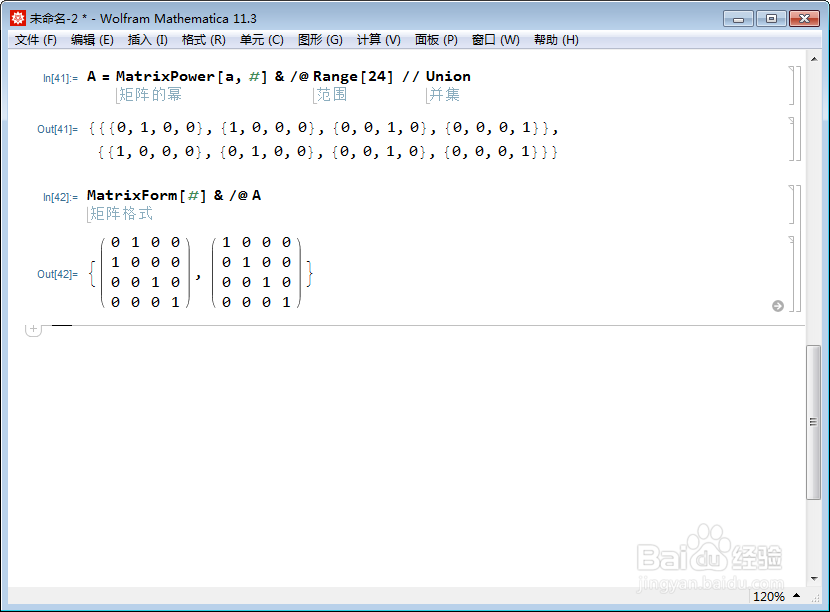
4、根据a和b，并使用矩阵乘积，就可以算出s4的矩阵表示。先算出a生成的子群A：A = MatrixPower[a, #] & /@ Range[24] // Union并且证明了，a是2阶元素。

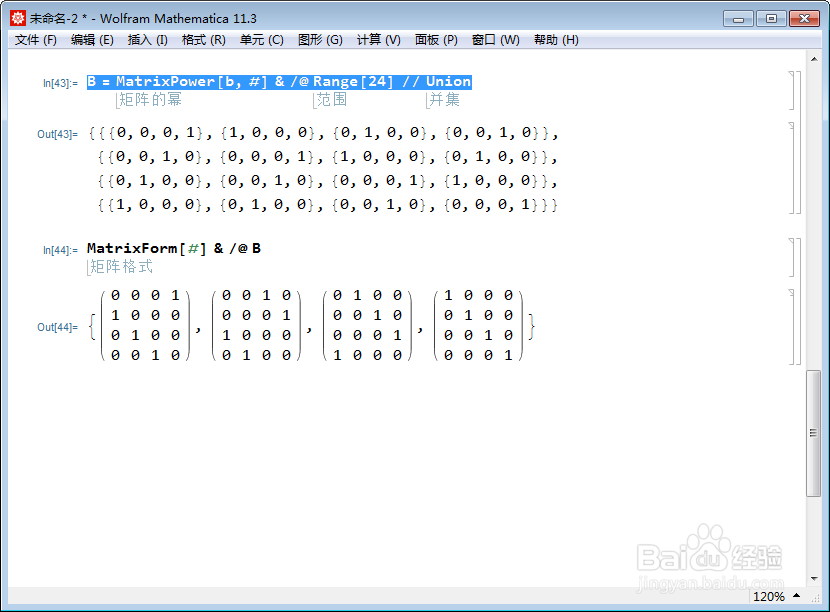
5、b生成一个四阶子群B：B = MatrixPower[b, #] & /@ Range[24] // Union

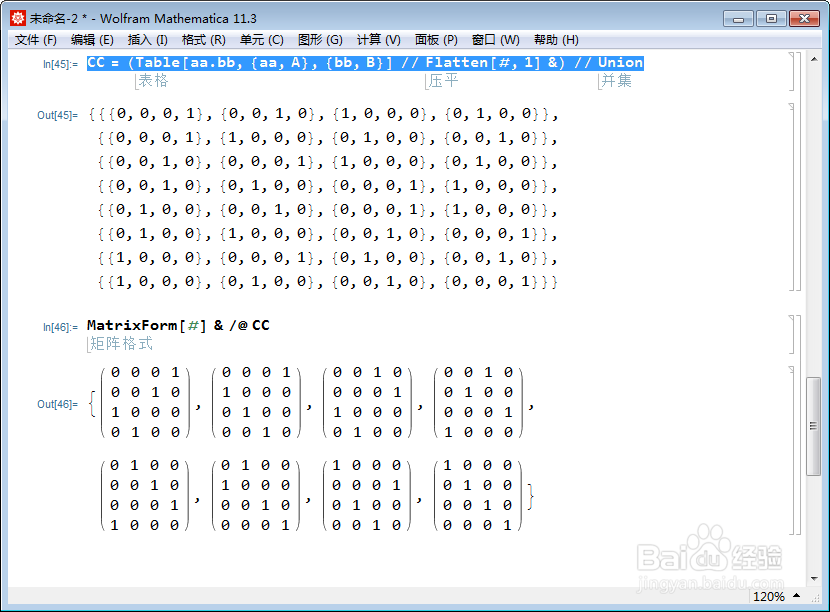
6、子睡连简郯群A和子群B的乘积：CC = (Table[aa.bb, {aa, A}, {bb, B}] // Flatten[#, 1] &) // Union读者可以自行验证，看看CC是不是群，是否满足群的基本定义。

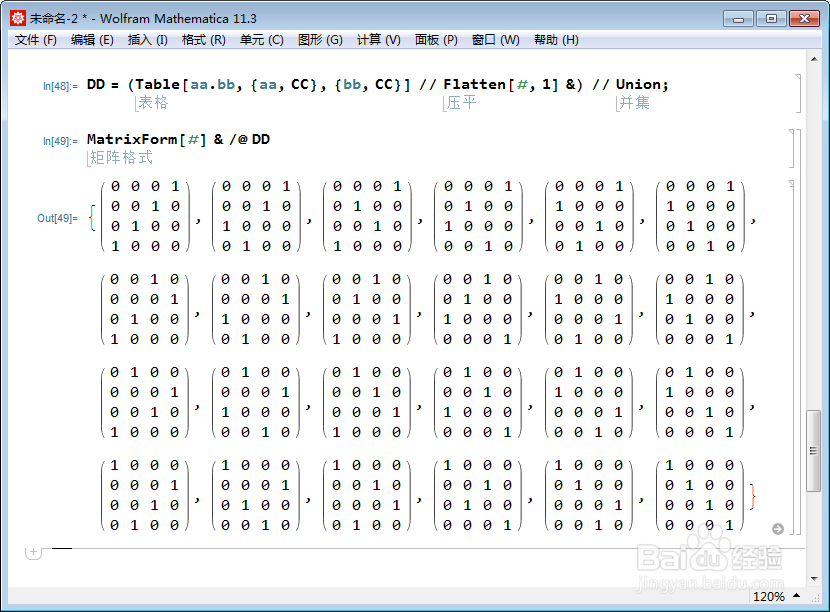
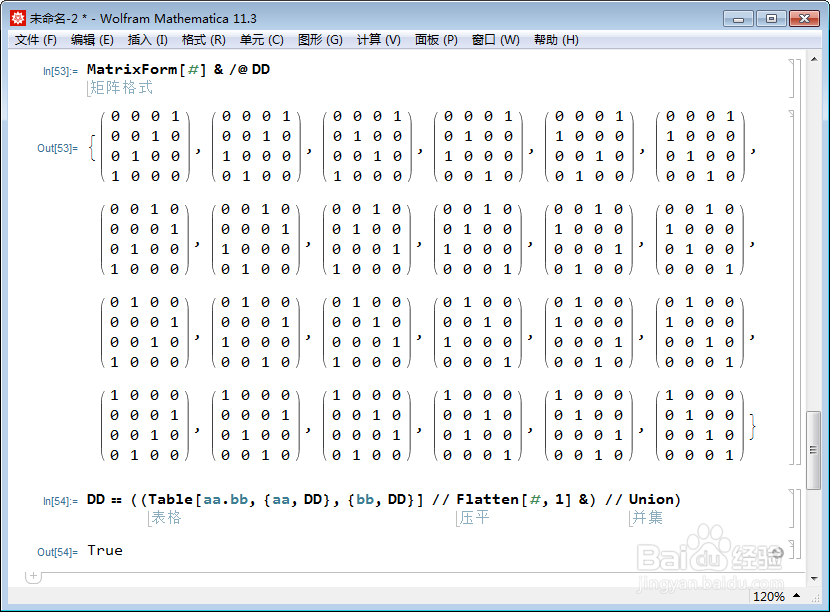
7、集合CC与CC的乘积，就得到s4的矩阵表示：DD = (Table[aa.bb, {aa, CC}, {b芟鲠阻缒b, CC}] // Flatten[#, 1] &) // Union;恰好24个不同的4阶矩阵。

8、为了证明DD是群，只需要验证DD=DD×DD即可：DD == ((Table[aa.bb, {aa, DD}, {bb, DD}] // Flatten[#, 1] &) // Union)