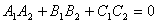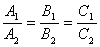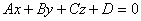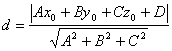高数～求过点(1,-4,5),且在各坐标轴上的截距相等的平面方程
所求的平面方程为：x陴鲰芹茯+y+z=2。
由空间平面的一般方程式：Ax+By+Cz+D=0，其中X,Y,Z轴的截距分别为：-A/D,-B/D,-C/D，因为其相等，设为k；栏硕沼桫又因为平面在各坐标轴上截距相等，且平面经过点(1，-4，5)；
则经过点（1，-4,5）的截距也是相等的，即k=各坐标之和，可得1-4+5=k，所以k=2
所以过点(1,-4,5),且在各坐标轴上的截距相等的平面方程为：x+y+z=2
扩展资料：
平面方程的类型
一、截距式
设平面方程为Ax+By+Cz+D=0,若D不等于0，取a=-D/A,b=-D/B,c=-D/C,则得平面的截距式方程：x/a+y/b+z/c=1 。它与三坐标轴的交点分别为P(a,0,0),Q(0,b,0),R(0,0,c)，其中，a,b,c依次称为该平面在x,y,z轴上的截距。
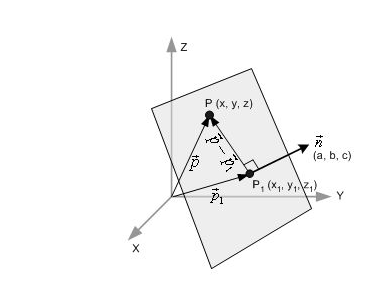
二、点法式
n为平面的法向量，n=(A,B,C),M,M'为平面上任意两点，则有n·MM'=0, MM'=(x-x0,y-y0,z-z0)，从而得平面的点法式方程：A(x-x0)+B(y-y0)+C(z-z0)=0 。三点求平面可以取向量积为法线任一三元一次方程的图形总是一个平面，其中x,y,z的系数就是该平面的一个法向量的坐标。
平面方程的特点：
设平面1和平面2的法向量依次为n1＝{A1,B1,C1}和n2＝{A2,B2,C2}
1.两平面垂直：
2.两平面平行：
3.平面外一点到平面的距离公式：设平面外的一点P0（x0，y0，z0），平面的方程为
平面方程的解法：
方法一：带入消元法。将条件中给出的点坐标等带入一般方程，求解系数。一般的方程都可以用此解法。
方法二：法向量解法。可以利用法向量和平面的系数关系，求解平面的系数
方法三：克莱姆法则。研究了方程组的系数与方程组解的存在性与唯一性关系;与其在计算方面的作用相比，克莱姆法则更具有重大的理论价值，用克莱姆法则求解时计算量较大，需要慎重选择。
参考资料：