怎样在学习中举一反三、触类旁通

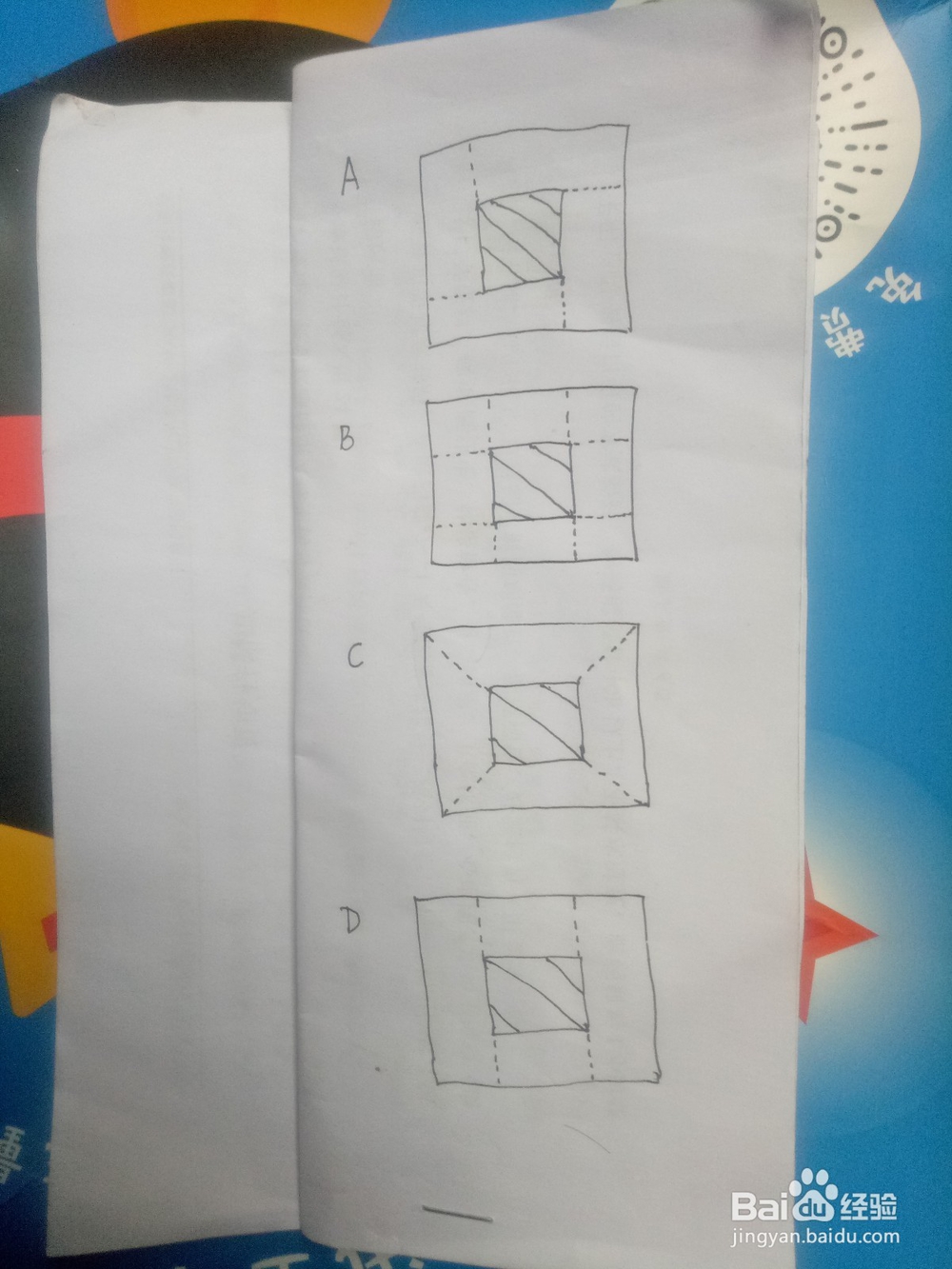
1、我们先直接来看看一道小学的题，不是什么难题怪题，而是正儿八经的基础题，做这道题再简单不过，但是我们的根本目的不是做题，而是通过做题你能学到什么，得到什么启示。学校操场有一个如图的正方形花坛，边长为20m，在花坛的四周有一条宽2m的小路，小路的面积是多少平方米？画出对应思路。（为便于作图，仅作草图，不按实际比例）

2、我们先对题目做出解答，如下图所示：A分割成四个相同的长方形；B分割为四个相同的长方形和四个相同的正方形；C分割为四个相同的梯形；D分割为两个大的长方形和两个小的长方形。（辅助线方向可能不一样，但是解答中的思路都一样）正方形、长方形、梯形的面积公式就不必提了，跟1+1=2一样简单的东西自然没什么可说的。

3、当时一位朋友帮她儿子向我问这道题，估计她不是没认真学，就是彻底遗忘成了一张白纸，这道题本身非常非常简单，我个人而言，粗略扫视烙疋艘烯题目第一反应是外面的大正方形减去里面小正方形即可，但是我们的根本目的是学到题以外的东西，那样才有意义。就我个人的思考来说，有这样几点信息：1、转化：化整为零、化繁为简、化不规则为规则；将复杂问题分割或者分解为简单问题。2、辅助线的应用：这对于后面中学平面几何和立体几何的学习尤为重要。3、叠加消除：本题是大正方形消除小正方形。

4、我们做题就应该深入思考，什么是思考，不是把题做对，而是从题里学习归纳总结出了什么有重要价值的方法、思路，这样我们再碰到这样一类题的时候根本不需要再做，一眼看穿，甚至在后面更高层级的学习中都依然能轻松应对，这才是真正的思考！我们需要的不是题海，而是少而精的经典！学会了深入思考，站在了一定高度后，很多的东西也就跟1+1=2一样简单了。会当凌绝顶，一览众山小。