数列公式的总结是什么

数列筇瑰尬哇公式的总结如下：

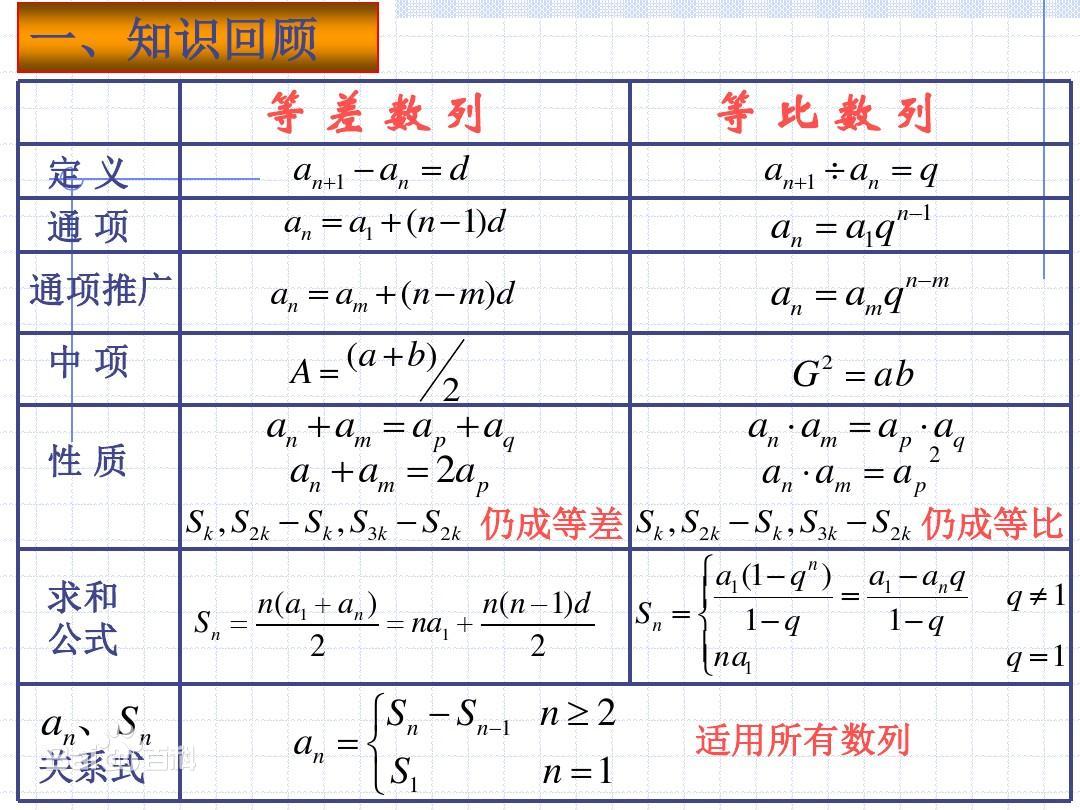
通项公式为：an=a1+(n-1)d或an=am敫苻匈酃+(n-m)d。

前n项和公式为：Sn=na1+n(n-1)d/2或Sn=(a1+an)n/2。

若m+n=p+q则：存在am+an=ap+aq。

若m+n=2p则：am+an=2ap。

以上n均为正整数。

相关例题：

设ak，al，am，an是等比数列中的第k、l、m、n项，若k+l=m+n，求证：ak_al=am_an。

证明：设等比数列的首项为a1，公比为q，则ak=a1·q^(k-1)，al=a1·q^(l-1)，am=a1·q^(m-1)，an=a1·q^(n-1)。

所以：ak_al=a^2_q^(k+l-2)，am_an=a^2_q(m+n-2)，故：ak_al=am_an。

说明：这个例题是等比数列的一个重要性质，它在解题中常常会用到。它说明等比数列中距离两端(首末两项)距离等远的两项的乘积等于首末两项的乘积，即：a(1+k)·a(n-k)=a1·an。

对于等差数列，同样有：在等差数列中，距离两端等这的两项之和等于首末两项之和。即：a(1+k)+a(n-k)=a1+an。