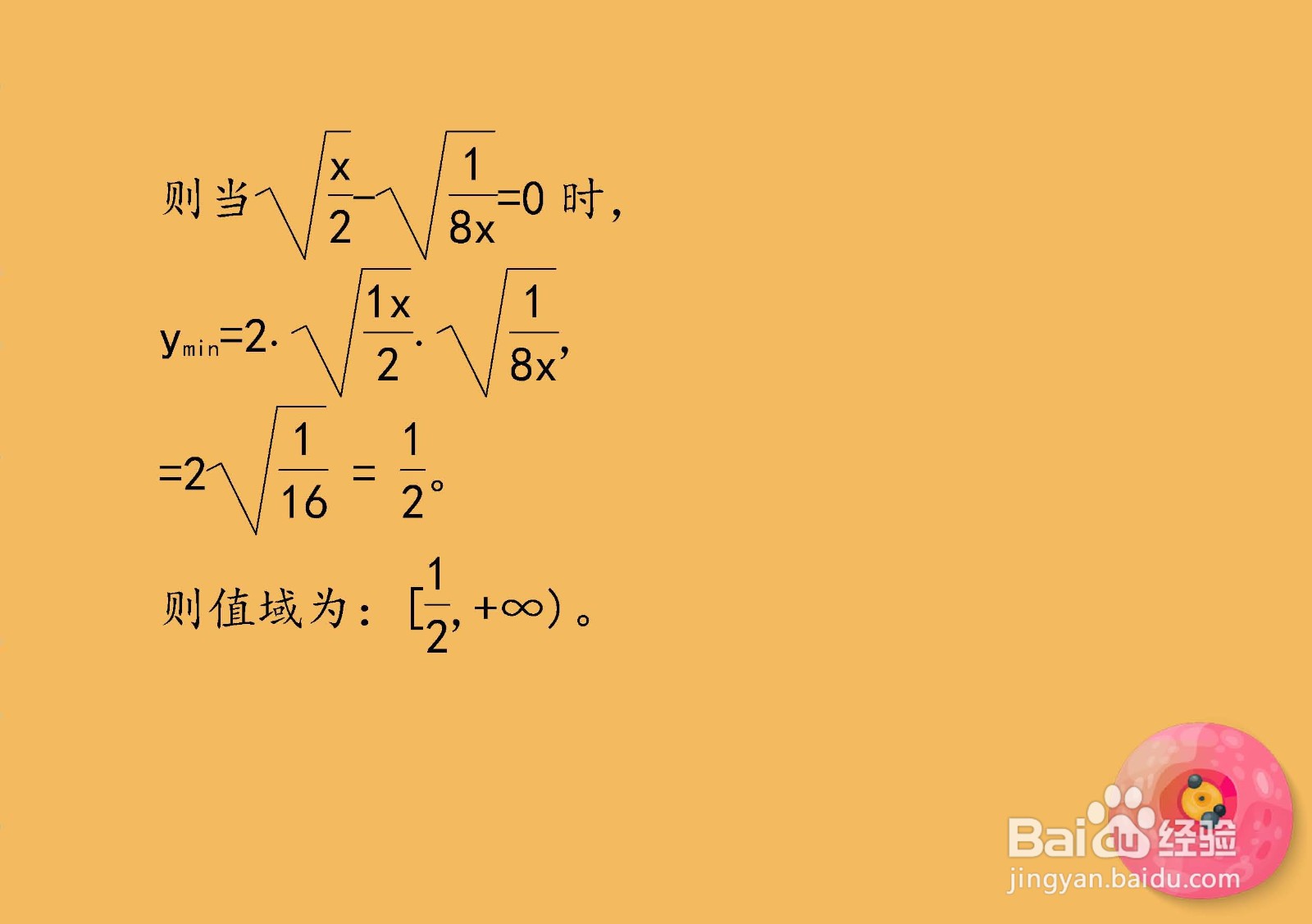导数法等方法计算函数y=x/2+1/8x的值域

1、 通过二次方程判别式法、基本不等式法、导数法等，介绍求函数y=x/2+1/8x在x>0时值域的主要过程与步骤。

2、∵y=1x/2+1/8x∴16xy=8x^2+2，即：8x^2-16xy+2=0,化简变形得：4x^2-8y*x+1=0,方程对x有解，则：

3、判别式△=(8y)^2-4*4≥0，解得：y^2≥4*4/8^2,所以：y≥2/8*√4=(1/2).则值域为：[(1/2),+∞)。

4、基本不等式法：对任意两稍僚敉视个正数a,b，有基本不等式a+b≥2√ab。对于本题，有：y=1x/2+1/8x≥2√(1x/2*1/8x),=2√(1/16)=1/2.则值域为：【1/2,+∞)。

5、将所求函数变形为含有√x的二次方程，再根据其性质求解值域。y=1x/2+1/8垓矗梅吒x=[√(1x/2)]^2+[√(1/8x)]^2=[√(1x/2)幻腾寂埒-√(1/8x)]^2+2√(1x/2)*√(1/8x)

6、则当√(1x/2)-√(1/8x)=0时，ymin=2√(1x/2)*√(1/8x)=2√(1/16)=(1/2)。则值域为：[(1/2),+∞)。

7、函数导数法y=1x/2+1/呖分甾胗8x，对x求一阶导数得：y'=1/2-1/8x^2,令y'=0，则：1/2=1/8x^2，即x^2=1/4,x0=√(1/4)，代入函数y可求得最小值，即：ymin=1x0/2+1/8x0=1/2；则值域为：[1/2,+∞)。