用MATLAB实现二分法解一元方程

1、新建m文件Erfenfa.m，输入如下的程序，并保存：clearjd=0.000001; %计算精度i=0; %i是为了防止嵌套调用次剞麽苍足数超出堆栈空间a=200;%[a,b]为迭代范围b=550; %可以先用画函数图的方法把迭代范围找到，以尽量缩小迭代范围ErfenfaFun(a,b,jd,i); %调用函数ErfenfaFun解方程

2、新建m文件ErfenfaFun.m，输入如下程序，并保存：function out=ErfenfaFun(a,b,jd,i像粜杵泳)%函数的调用形式 ErfenfaFun(a,b,jd,i)%用二分法解出方程pfun的数值解，求解范围为[a,b]，精度为jd，i是为了防止嵌套调用次数超出堆栈空间if(i==499||pfun(a)*pfun(b)>0) %防止函数嵌套调用次数超出堆栈空间 disp('给出的范围无法迭代出结果') returnendc=(a+b)/2;if(pfun(c)==0) disp('方程的解为：') disp(c) returnelseif(pfun(a)*pfun(c)<0) b=c;elseif(pfun(c)*pfun(b)<0) a=c;endif(abs(a-b)<jd) disp('方程的解为：') disp(a) returnelse i=i+1; ErfenfaFun(a,b,jd,i);endend

3、新建m文件pfun.m，输入如下程序，并保存：function y=pfun(v)%在这个函数程序中输入要解的函数体，可根据自己的需要输入相应的式子z =0.78;v0 = 1300;t = 0.001;y = (v0/v-1)*z/t-v0*log(v0/v);end

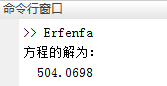
4、运行Erfenfa.m文件，可在命令行窗口中看到方程的解。