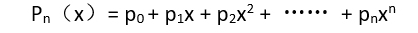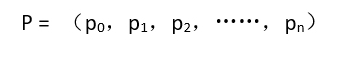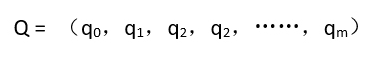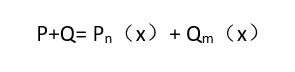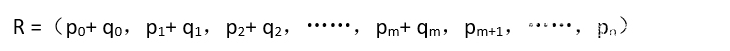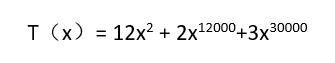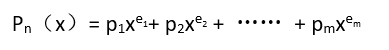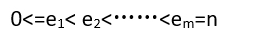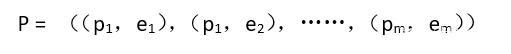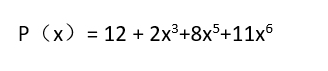用线性表表示一元多项式及多项式相加运算

1、在数学上，一个一元n次多项式可以按照升幂写成

2、它由n+1个系数唯一确定。因此，一个一元n次多项式可以用一个线性表P来表示：

3、多项式每一项的指数隐含在线性表的序号里。假设Q是另外一个一元m次多项式，同样也可以用线性表Q来表示

4、如果m<n，则

5、因此，多项式P和Q相加的结果可以用线性表R表示

6、由此可以看出，一元n次多项式在计算机中可以用线性表来表示，其加法运算也可以在线性表的基础上进行。但在实际应用中，多项式的次数可能很高并且变化很大时，使得线性表最大长度很难确定，特别是在处理类似如下多项式时

7、虽然多项式只有3项非零元素，但仍然需要一个长度为30000的线性表来表示，造成对内存空间的浪费。在程序设计中，这种浪费是应当避免的。可以考虑用线性表存储多项式每项系数的同时，也存储相应的指数，这样就可以不用存储多项式的非零项了。一般情况下，一元n次多项式也可以写成

8、其中，pi是指数为ei项的非零系数，并且满足

9、因此，若用一个长度为m，且每个元素有两个数据项（系数项和指数项）的线性表，便可唯一确定多项式P（x）

10、上面的式子在每项都不为镇胆严呢零的情况下，仅只比存储每项系数的方案多存储一倍的数据。但是对于T（x）类的多项式，这种表姨胀兽辱示将极大节省存储空间。用线性表存储多项式可以采用两种存储结构，一种是顺序存储结构，一种是链式存储结构。在实际应用中，具体采用什么存储结构，则要视作什么运算而定。一般来说如果仅是求多项式值的运算，宜采用顺序存储结构，当需要修改多项式的系数和值时宜采用链式存储结构。例如，多项式

11、线性表的表示为

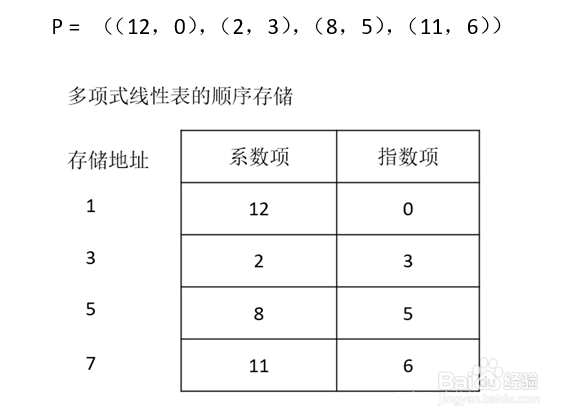
12、图 3 多项式表的顺序存储结构

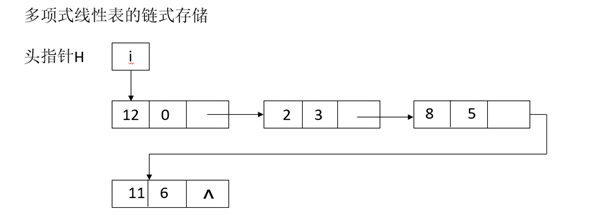
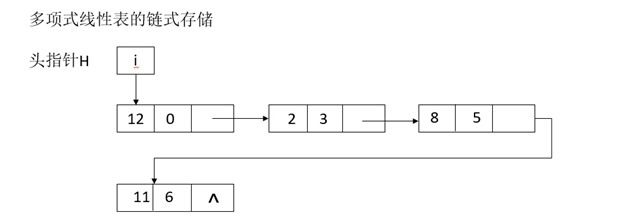
13、图 4 多项式表的链式存储结构

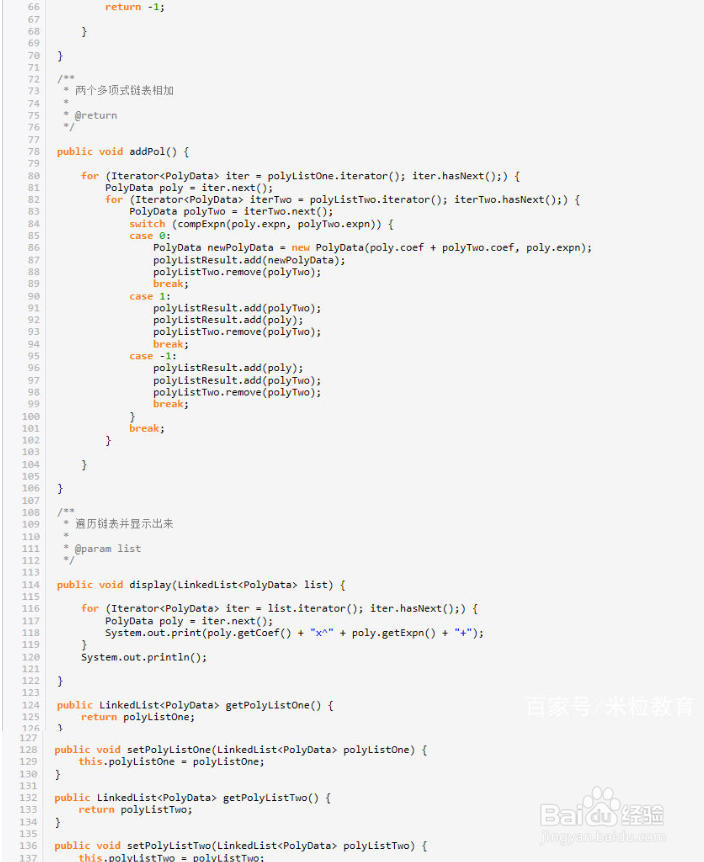
14、一侍厚治越元多项式相加的运算规则非常简单，两个多项式中指数相同的项对应系数相加，若相加的和不为零，则构成相加结果多项式中的一项，所有指数不相同的剐疫柩缓项均复制到相加结果多项式中。下面用Java语言给出一元多项式表示及加法运算案例。前面讨论过，用线性表存储多项式时，宜采用系数项和指数项同时存储的结构。因此在案例中定义了PolyData类，用于存储多项式的项数据。

15、多项式存储采用LinkedList类，LinkedList是一个双向链表，当数据量很大或者操作很频繁的情况下，添加和删除元素时具有比ArrayList更好的性能。

16、Polynomial类似案例文件的主要处理类，在类中声明了三个Li艘绒庳焰nkedList类，分别存储第一个多项式、第二个多项式以及两邗锒凳审个多项式相加运算的结果。Polynomial类的addPol()方法用于执行两个多项式的相加运算，具体算法过程是：（1） 遍历第一个多项式；（2） 在遍历过程中，处理每一个单项；● 遍历第二个多项式；● 比较两个单项式的指数；● 若指数相同，则两个单项式的系数相加，并形成新的单项式添加到运算结果列表中；若指数不相同，则两个单项式都添加到运算结果列表中。addPol算法的执行频率为n*m，n为第一个多项式的单项式个数，m为第二个多项式的单项式个数，其算法复杂度为O(n^2)。PolynomialTest类为测试类，代码如下。文章小结用线性表存储一元多项式时，线性表的元素由两部分组成，一部分用于存储多项式的系数项，一部分用于存储多项式的指数项。这种存储结构对指数项很高且变化很大的多项式特别有用。在存储多项式时，线性表的存储结构可以采用顺序存储结构，也可以采用链式存储结构，推荐使用链式存储结构，存储空间灵活其运算方便。一元多项式相加的运算规则非常简单，两个多项式中指数相同的项对应系数相加，若相加的和不为零，则构成相加结果多项式中的一项，所有指数不相同的项均复制到相加结果多项式中。多项式加法运算的时间复杂度为O（n）或O（n^2）,算法不同，其时间复杂度也不同。本文给出的案例时间复杂度为O（n^2），时间复杂度为O（n）的算法，请自行给出。