如何快速理解笛卡尔积的概念

1、首先瞧一眼定义：设D1,D2,...,Di,...,Dn为任意集合，定义D1,D2,...,Di,...,Dn的笛卡尔积为D1×D2×...×Di×...×Dn={(d1,d2,...,di,...,dn)|di∈Di，i=1,2,3，...，n}其中，每一个元素（d1,d2,...,di,...,dn）称为一个n元组（n-tuple，即属性的个数），元组的每一个di称为元组的一个分量。若Di(i=1,2,3,...,n)为有限集，其基数（cardinal number，即元组的个数）为mi(i=1,2,3,...,n)，则D1×D2×...×Di×...×Dn的基数为各基数之积，笛卡尔积可以用二维表来表示。这一看太麻烦了，太抽象了，简直劝退。所以，我们暂且不管。

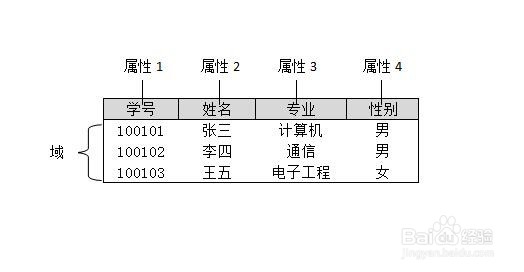
2、我们描述一个事物，可以用其中若干特征来表示，这些特征称为属性（Attriubute）。比如描述学生，学生的属性有姓名，性别，身份证号，职业等等，描述苹果，属性有颜色，味道，出产地等等。同时，每个属性有取值范围，取值范围可以看做是一个值的集合，称为该属性的域（domain）。比如，性别的域为{男，女}，也就是说性别的取值范围是男，女；颜色的域也可以为{赤，橙，黄，绿，青，蓝，紫}，也就是说颜色的取值范围是赤，橙，黄，绿，青，蓝，紫；个位整数的域为{0，1，2，3，4，5，6，7，8，9}等等。因此，在笛卡尔积定义中用字母D代表域，D可以看成是取值范围，集合，或空间。看哪个好理解了。

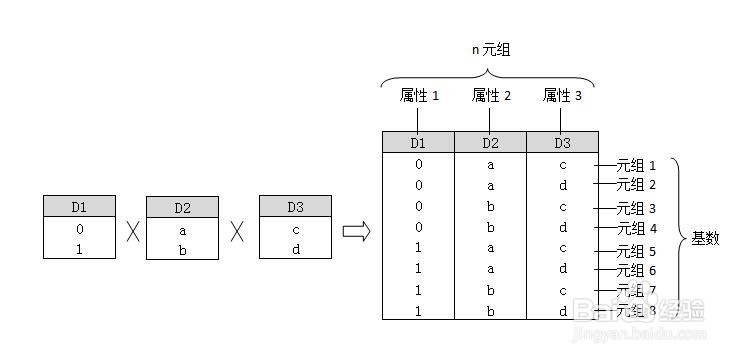
3、接下来，看个例题来理解概念：若D1={0,1},D2={a,b},D3={c,d},求D1×D2×D3。我们来分析：D1的取值范围为{0,1}D2的取值范围为{a,b}D3的取值范围为{c,d}根据定义，这有三个域D1,D2,D3相乘，笛卡尔积的每一个元素将会是（d1,d2,d3)的形式，也就是一个三元组。元组的每个值di都称为元组的一个分量，而每个分量分别来自不同的域D1,D2,D3。所以，D1×D2×D3={(0,a,c),(0,a,d),(0,b,c),(0,b,d),(1,a,c),(1,a,d),(1,b,c),(1,b,d)}它的基数为2×2×2=8，也就是元组的个数为8，用二维表表示的行数为8。