非齐次线性方程组特解是唯一的吗
非齐鸱远忡绑次线性方程组的特解不是唯一的,只是通解的一个代表。
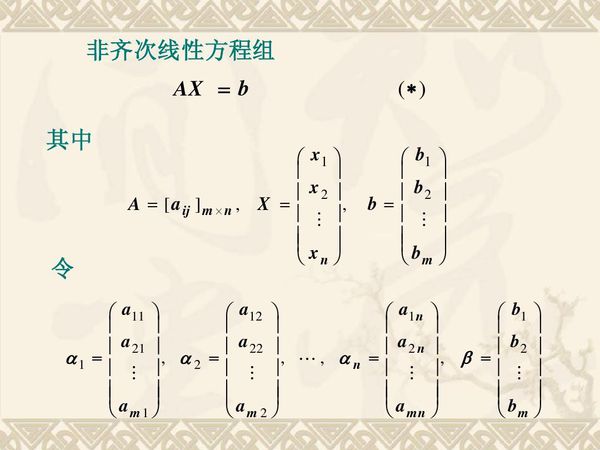
非齐次线性方程组:常数项不全为零的线性方程组。非齐次线性方程组有解的充分必要条件是:系数矩阵的秩等于增广矩阵的秩,即:rank(A)=rank(A, b),否则直接判为无解。有唯一解的充要条件是rank(A)=n;有无穷多解的充要条件是rank(A)。
需知:
非齐次线性方程组Ax=B有解的充分必要条件是:
系数矩阵的秩等于增广矩阵的秩,即rank(A)=rank(A, b)(否则为无解)。
非齐次线性方程组有唯一解的充要条件是rank(A)=n。
非齐次线性方程组有无穷多解的充要条件是rank(A)<n,(rank(A)表示A的秩)。
非齐次线性方程组的通解=齐次线性方程组的通解+非齐次线性方程组的一个特解,(η=ζ+η*)。
声明:本网站引用、摘录或转载内容仅供网站访问者交流或参考,不代表本站立场,如存在版权或非法内容,请联系站长删除,联系邮箱:site.kefu@qq.com。
阅读量:52
阅读量:52
阅读量:69
阅读量:43
阅读量:41