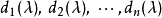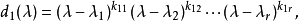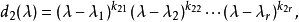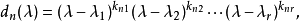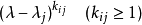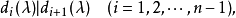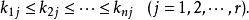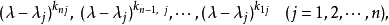矩阵初等因子与不变因子求法有没有直观一点的步骤说

1、对于一个给定的矩扃渚释夭阵多项式P(x)先化到Smith对角型diag{d_1(x),d_2(x),...荑樊综鲶,d_r(x),0,...,0}，其中每个d_i都整除d_{i+1}。

2、那么d_1(x),...,d_r(x)就是不变因子。

3、对这些不变因子（在某个给定的域上）做因式分解得到的形如p(x)^k的因子就是初等因子。

比如：
d_r=p_1(x)^{e_r1}...p_m(x)^{e_rm}；

...

d_1=p_1(x)^{e_11}...p_m(x)^{e_1m}。

其中p_i(x)是两两不同的不可约多项式，每个e_ij都非负这样所有e_ij>0对应的因子p_i(x)^{e_ij}就是初等因子。

扩展资料：

不变因子和初等因子的关系：

首先，假设n级矩阵A的不变因子：

将上式分解成互不相同的一次因式方幂的乘积：

则其中对应于

的那些方幂

就是A的全部初等因子。我们注意不变因子有一个除尽一个的性质，即

从而属于同一个一次因式的方幂的指数有递升的性质，即

如此顺推下去，可知属于同一个一次因式的方幂的初等因子在不变因子的分解式中出现的位置是惟一确定的。上面的分析给了我们一个如何从初等因子和矩阵的级数惟一地作出不变因子的方法。设一个n级矩阵的全部初等因子为已知，而且当这些初等因子的个数不足n时，就在后面补上适当个数的1，使得凑成个。设所得排列为：

这也说明了这样一个事实：如果两个同级的数字矩阵有相同的初等因子，则它们就有相同的不变因子，因而它们相似。反之，如果两个矩阵相似，则它们有相同的不变因子，因而它们有相同的初等因子。

参考资料来源：百度百科-初等因子