关于任意时刻太阳高度的计算问题
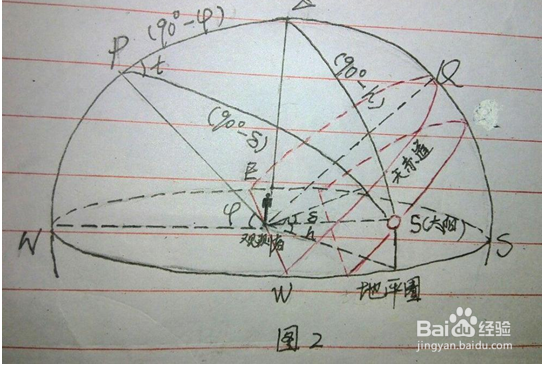
1、方法一:解天文三角形太阳高度的大小与三个因素有关:①当地纬度②太阳赤纬(即直射点纬度)③太阳时角(即太阳在周日圈上的位置)根据这三个变量,我们可以在天球上建立一个球面三角形。如图,Q为上点,P为天极,Z为天顶,S为太阳。将太阳、天极、天顶二者连接起来可以构成一个球面三角形。这个球面三角形的三边由午圈、时圈和平经圈的弧段构成,称为天文三角形和ZPS角形。其中,弧PZ为天顶极距,即当地纬度的余角(90º-φ)。弧ZS为太阳的天顶距,即太阳高度的余角(90º-h)弧PZ为太阳的极距,即太阳赤纬的余角(9oº-δ)。t为当时太阳的时角。在这个球面三角形中,已知三边及一夹角可代余弦公式:cos(90º-h)=cos(90º-φ)cos(90º-δ)+sin(90º-φ)sin(90º-δ)cost将上式化简得sinh=sinφsinδ+cosφcosδcost即h=arcsin(sinφsinδ+cosφcosδcost)这就是计算任意时刻太阳高度的公式。如果你使用过这个公式,去发现它有一个致命的缺陷,就是参数代入后无法计算出正确的数值。最终也只能在特殊角的情况下估值,所以我们要探究其他计算方法。
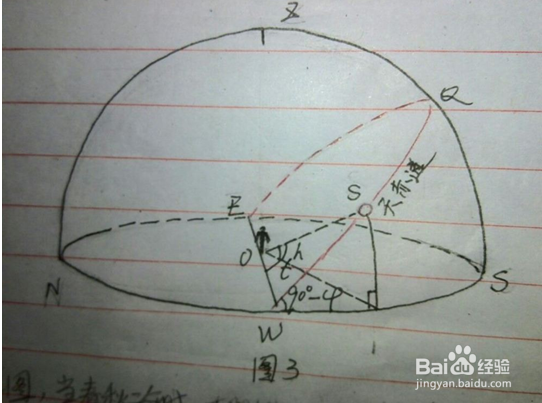
2、方法二:重建球面三角 前面用解天文三角法推导出来了公式无法计算出结果,或许球面三角的建立的问题。所以我们可以重建球面三角。如图,当二分日,太阳周日圈与天赤道重合,因此我们不用考虑太阳赤纬。过太阳S作与地平圈垂直的弧段,交地平圈于点P。(图中未注明,自行脑补),以太阳周日圈、平经圈、地平圈的弧段为三边组建一个球面三角形。S为太阳,O为观测者,W为西点。t为从日出时刻到该时刻太阳扫过的圆心角的度数,即(该时刻-日出时刻)*15º,h为当时的太阳高度角,天赤道与地平圈的夹角为当地纬度的余角,即90º-φ。在球心三面角0-WpS中,已知两角及一边,可代正弦公式:sint/sin90º=sinh/sin(90º-φ)变形及化简后得h=arcsin(sintcosφ)上式就是计算二分日任意时刻太阳高度的公式。但是,重建的球面三角只能用于二分日任意时刻太阳高度的推算。如果不是二分日,太阳轨道平面则未过天球球心。这时还需要考虑太阳赤纬,然而太阳赤纬与太阳扫过的角度、周日圈与地平圈的夹角不能组建为一个球面三角形。所以无法计算。我们还需探究其他的方法。
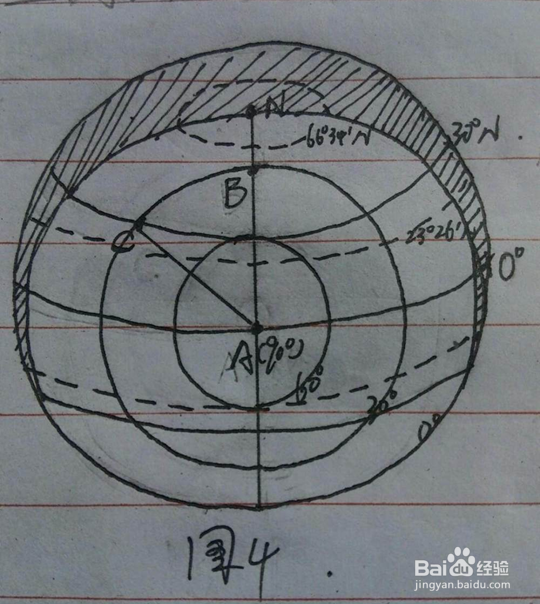
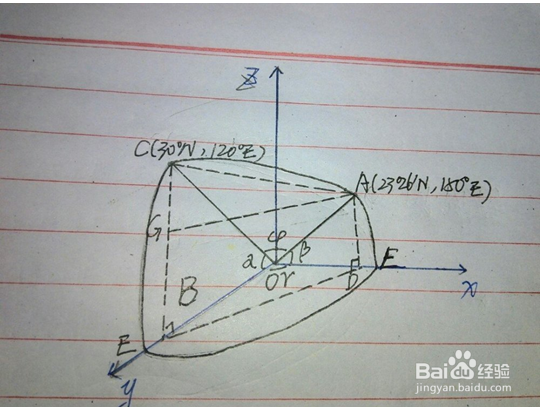
3、方法三:利用等太阳高度线原理计算太阳高度差前面两种方法都是从太阳视运动的角度去考虑的,都无法计算出任意时刻的太阳高度,也许我们可以尝试从太阳孕驷巴墟高度的分布这个角度去考虑。我们知道,任何时刻太阳只能照亮地球的一半。在昼半球,晨昏线上的太阳高度为0º,太阳直射点为90º。太阳高度由太阳直射点向晨昏线(圈)有规律的递减。我们将昼半球太阳高度相等的点连接起来,就得到了以太阳直射点为中心呈同心圆分布的等太阳高度线图。我们知道,两地正午太阳高度差等于纬度差。如下图,A、B两地同在太阳直射的经线上,若A、B两地纬度相差50º,则B地与直射点A地太阳高度相差50º,B地的太阳高度为H=90º-50º=40º。同理,将地球表面的A、C两地连接起来,得到弧AC。由于弧AC是过地心大圆的弧段,因此,可以将A、C两地看成是同一经线上的。这时,只要我们求出弧AC所对圆心角的度数,便可得知c地与直射点A的太阳高度差,从而算出C点的太阳高度。用此方法计算任意时刻的太阳高度分为以下几个步骤:1.算太阳直射点的经纬度。太阳直射点的经度可以根据你所在地的地方时来推算,纬度则利用日期推算。公式为C=arcsin(sinAsinB)。A:从春分日起算到该日天数/半年天数*πB:黄赤交角2.计算该地与太阳直射点的最短距离(或最短距离所对的圆心角度数),得到两地太阳高度差。具体方法等会详细介绍。3.算该地太阳高度。H=90º-太阳高度差。例:某地的经纬度为(30ºN,120ºE),求该地夏至日上午10:00的太阳高度?根据地方时算太阳直射点的经度。120ºE+(2*15º)=150ºE所以太阳直射点的地理坐标为[23º26′N,150ºE]。计算两地最短距离所对的圆心角,这个我要详细说一下。首先,我们要以地心为原点建立一个空间直角坐标系。将A、c两地及其所在经线与赤道的交点与地心连接起来,并过点A、C作赤道半径OE、OF的垂线,垂足为B、D。过点A作CB的垂线,垂足为G。α为C地的纬度,β为A地的纬度,γ为两地经度差。φ就是我们要求的圆心角。在Rt△COB中CB=Oc*sinα=6371*sin30º=3185.50kmOB=√(Oc^2-CB^2)=√(6371^2-3185.50^2)≈5517.45km在Rt△AOD中AD=OA*sinβ=6371*sin23º26′≈2533.63kmOD=√(OA^2-AD^2)≈5845.54km在△BOD中BD=√(OD^2+OB^2-2*OB*OD*cosγ)=√(5845.54^2+5517.45^2-2*5517.45*5845.54*cos30º)≈2957.98km在Rt△AGC中CG=CB-GB=3185.50-2533.63=651.87kmGA=BD=2957.98kmAC=√(CG^2+GA^2)=√(651.87^2+2957.98^2)≈3028.96km在△AOC中φ=arccos[(Oc^2+OA^2-AC^2)/(2*OC*OA)=27º30′故该地的10:00的太阳高度为H=90º-27º30′=62º30′可见,难度最大的就是计算两地球面最短距离的圆心角,当然,如果嫌麻烦也可以不使用我的方法,计算两地最短球面距离有公式:设A、B经纬度为(jA,WA)(jB,WB),则半径为R球面上两点间最短距离为弧AB=R*arccos[sin(WA)sin(WB)+cos(WA)Cos(WB)c0S(jA-jB)]求出弧长再转化为圆心角的度数就可以了。