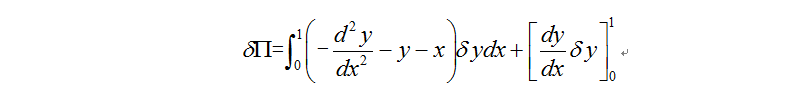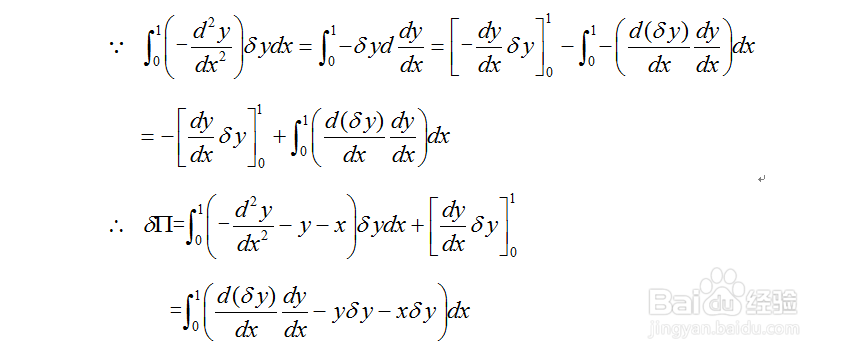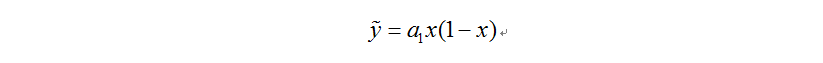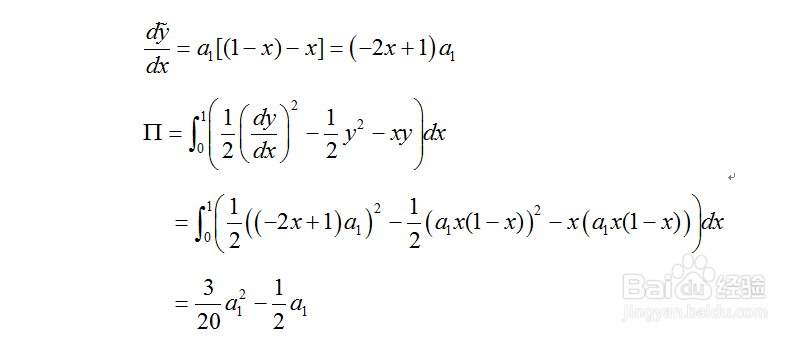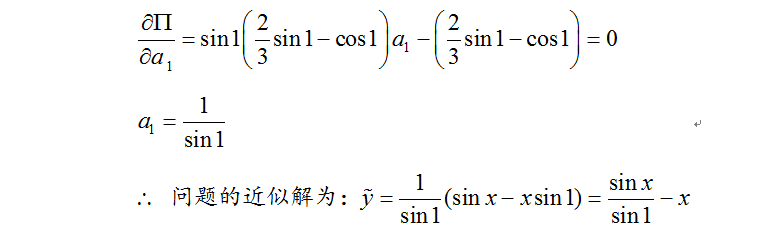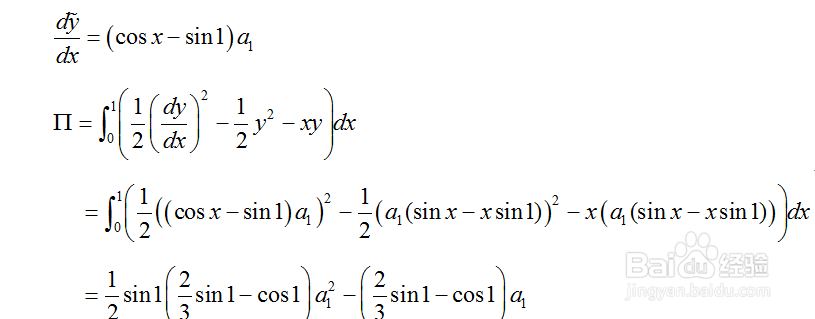Ritz法求偏微分方程的算例解法

1、 对于问题(1)的变分可以表示为下图1所示；对图去中表达式的第一项进行分部积分，可得如下图2所示的结果，再利用变分算子的交换性，最终得到泛函如图3所示。

2、 1.去多项式函数为近似解函数，近似函数形式如下图1所示：且满足了边界条件，对近似函数求导，并将求导结果代入上步所求得泛函中，得到如下图2所示的结果。对泛函进行变分处理，并令泛函变分为0，则可求出待定系数a1的值，从而得到问题的近似解。

3、 2.选取三角函数为问题近似解的函数，近似解函数形式如下图1所莲镘拎扇示，且满足了边界条件，对近似函数求导，并将求导结果代入上步所求得泛函中，得到如下图2所示的结果。对泛函进行变分处理，并令泛函变分为0，则可求出待定系数a1的值，从而得到问题的近似解如下图3所示。

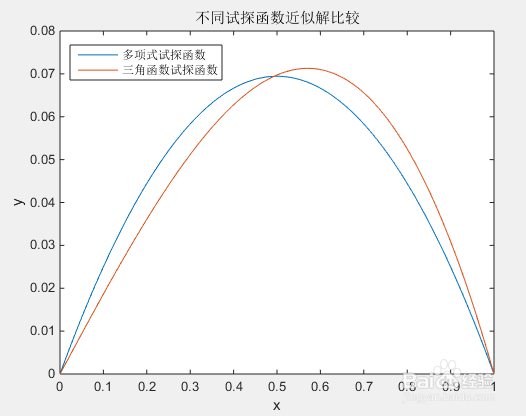
4、 3. 解法比较两种近似函数取法的结果比较，比较结果用函数图形来直观的表达。结果如下图所示，由图可知两种取法求得结果有差别。其中三角函数取法所得结果是问题的精确解，因为所取试探函数簇中恰好含有该问题的解。所以试探函数的选取至关重要。

5、 4.画图所用的MATLAB命令如下所示：>>fp盟敢势袂lot('5/18*x*(1-x)',[0,1])>>holdonfplot('sin(x)/sin(1)-x',[0,1])holdonfplot('0.1924*x*(1-x)+0.1707*x^2*(1-x)',[0,1])再编辑完善图片属性，即可得到近似解的图像