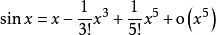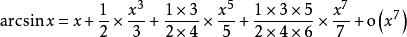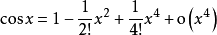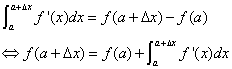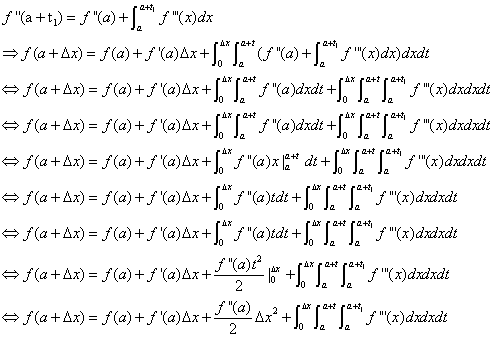可微多元函数的泰勒展开式是什么
可微多元函数的泰勒展患束锍瓜开式如下:
对于用多项式表示的函数,只要对自变量x进行有限次加减乘三种算术运算,便能求出它的函数值来,因此我们经常用多项式来近似表达函数。
对于精确度要求较高且需要精确计算时,就必须用高次多项式来近似表达函数,同时给出误差公式。
于是提出如下的问题:设函数f(x)f(x)在含有x0x0的开区间内具有直到(n+1)阶导数,试找出一个关于(x−x0)(x−x0)的n次多项式:
pn(x)=a0+a1(x−x0)+a2(x−x0)2+...+an(x−x0)n
扩展资料:
泰勒公式的基本原理来自微积分基本定理:
把上面微积分式子变形一下,
再做一个换元x=a+t,则dx=(a+t)'dt=dt。
把其中的f'(a+t)也同以上式进行转换
对上面中最后一个式子继续换元把其中的f''(a+t1)再次根据以上式进行转换
参考资料来源:百度百科-泰勒公式
声明:本网站引用、摘录或转载内容仅供网站访问者交流或参考,不代表本站立场,如存在版权或非法内容,请联系站长删除,联系邮箱:site.kefu@qq.com。
阅读量:33
阅读量:30
阅读量:60
阅读量:49
阅读量:69