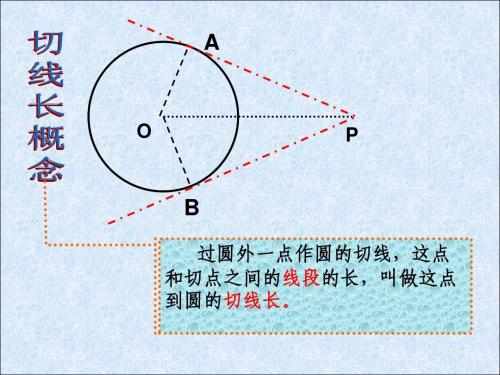
圆的切线方程 推导过程（思路即可）

设直帧霭绎郎线方程：y=k(x-x0)+y0

既然点在圆上，则圆心和切点连线的斜率k=(y0-b)/(x0-a) ，所以切线斜率：-1/k=(a-x0)/(y0-b) 所以切线方程：y=(a-x0)/(y0-b) *(x-x0)+y0

注意：求圆的切线，当已知切点时，用上述方法；当切点未知，即从圆外某点做切线，利用圆心到直线的距离等于半径求斜率。

研究切线以及切线的斜率方程，涉及几何、代数、物理向量、量子力学等内容。是关于几何图形的切线坐标向量关系的研究。分析方法有向量法和解析法。

扩展资料：

P和Q是曲线C上邻近的两点，P是定点，当Q点沿着曲线C无限地接近P点时，割线PQ的极限位置PT叫做曲线C在点P的切线，P点叫做切点；经过切点P并且垂直于切线PT的直线PN叫做曲线C在点P的法线（无限逼近的思想）。

说明：平面几何中，将和圆只有一个公共交点的直线叫做圆的切线．这种定义不适用于一般的曲线；PT是曲线C在点P的切线，但它和曲线C还有另外一个交点；相反，直线l尽管和曲线C只有一个交点，但它却不是曲线C的切线。