证明恒等式arcsinx+arccosx=π/2，(-1<=x<=1)

设f(x)=arcs坡纠课柩inx+arccosx，
∵f(x)在[-1,1]连续,在(-1,1)可导
∴f'(x)=1/√(1-x^2)-1/√(1-x^2)

由拉格朗日中值定理 一定可以在[-1,1]中找到一个a点
使得 f(a)=[f(1)-f(-1)]/(1-(-1))

∵导函数等于0 所以f(x)是常系数函数 即f(x)=a
∴x=0时 f(0)=arcsin0+arccos0=π/2
∴恒等式成立

扩展资料

微分中值定理是一系列中值定理总称，是研究函数的有力工具，其中最重要的内容是拉格朗日定理，可以说其他中值定理都是拉格朗日中值定理的特殊情况或推广。微分中值定理反映了导数的局部性与函数的整体性之间的关系，应用十分广泛。

如果函数f(x) 满足：

1)在闭区间[a,b]上连续；

2)在开区间(a,b)内可导。

那么：在(a,b)内至少有一点ξ(a<ξ<b)，

使等式 f(b)-f(a)=f′(ξ)(b-a) 成立。

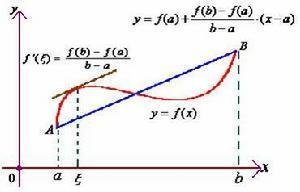
拉格朗日中值定理的几何意义是：曲线上必然存在至少一点，过该点的切线的斜率和连接曲线（a，b）的割线的斜率相同；或者说，曲线上必然存在至少一点可以做割线（a，b）的平行线

参考资料百度百科-微分中值定理