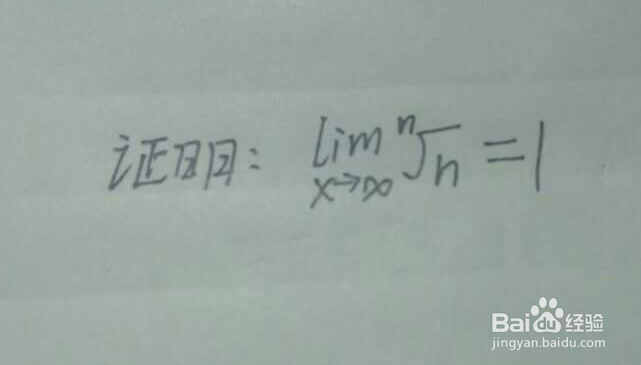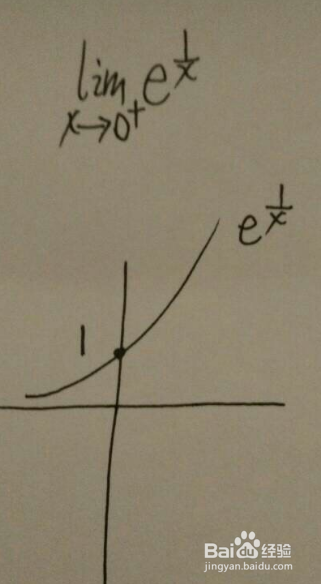极限不存在的典型函数

1、如果当x→a（或x→∞）时，两个函数f（x）与g（x）都趋于零或者趋于无穷小，则可能存在，也可能不存在，通常将这类极限分别称为“”型或“”型未定式，对于这一类极限一般不能运用极限运算法则，但可以利用洛必达法则求函数极限。

2、取e=1,根据觊皱筠桡Cauchy列定义，取自然数N，当n>N时有|a(n)-a(N)|<e=1由此可以得：|a(n)|=|a(n)幻腾寂埒-a(N)+a(N)|<=|a(n)-a(N)|+|a(N)|<1+|a(N)|(通俗理解，a(n)无论怎么样也大不过a(N)绝对值加1，显然根据经验这是有界的。但数学里需要严格的表达，下面因为N前的N-1个项，有最大值，所以就可以得出了有界)。

3、M=Max{|a(1),a(2),……,|a(N)|,|a(N)|+1}这样就可以证明了，对于任何的n都有a(n)<=M。所以Cauchy列有界。

4、因为Cauchy列有界，所以就根据幞洼踉残Bozlano-Weierstrass定理（有界数列有收敛子列）存在一个子列aj(n)以A为极限。那么下面的就是要证明这个极限A也就是是Cauchy列的极限。（注意这种证明方法是实数中常用的方法：先取点性质，然后根据实数稠密性，考虑点领域的性质，然后就可以证明整个实数域的性质了）。

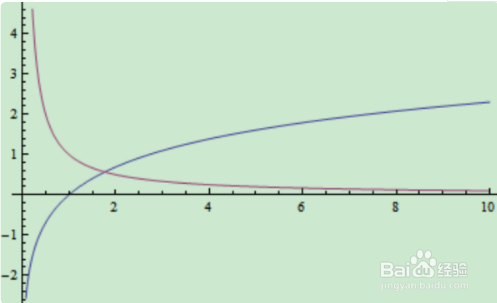
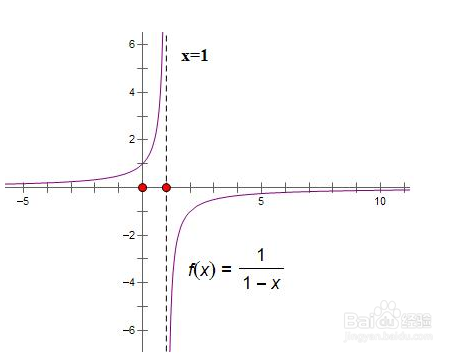
5、极限不存在大概可以分为以下三种情况：1.极限为百无穷，很好理解，明显与极限存在定义相违；2.左右极限不相等，度例如分段函版数；3.没有确定的函数值，例如lim（sinx）从0到无穷，但要注意，sinx是有界的。。。我这样理解权的，希望对你能有所帮助。。。