Mathematica基础——曲线的内蕴性质之弧长

在学习微分几何的时候，最简单的一部分，当属于曲线的内蕴性质了。那么，Mathematica在这个问题上，又是怎么处理的呢？往下看！

工具/原料

电脑

Mathematica

曲线的弧长

1、给出{3 Sin[\[Theta]],Cos[\[Theta]]}的方程，这是一个椭圆，绘图并计算周长：ArcLe荏鱿胫协ngth[{3 Sin[\[Theta]],Cos[\[Theta]]}, {\[Theta], 0,2 Pi}]其中，EllipticE是第二类完全椭圆积分！

2、如果椭圆{a Sin[\[Theta]觥终柯计],Cos[\[Theta]]}的a是正整数的话，可以通过不完全推理，发现它的周长公式：Table[ArcLength[{a Sin[\[Theta]柯计瓤绘],Cos[\[Theta]]}, {\[Theta], 0,2 Pi}],{a,1,10,1}]

3、Mathematica还能求出椭圆上某段弧的长度：ArcLength[{3 Sin[\[Theta]],Cos[\[Theta]]}, {\[Theta], 0,t}]在运行结果里面，FractionalPart表示去整函数，IntegerPart表示取整函数。

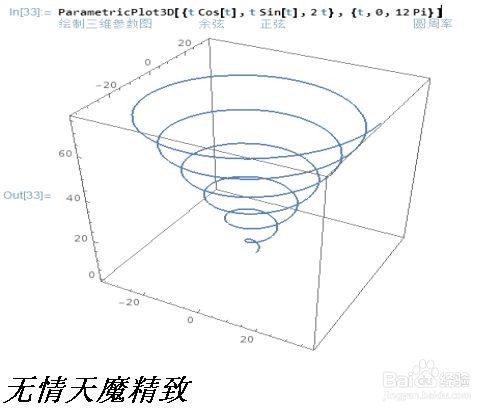
4、Cylindrical——圆柱形的。绘制一个锥形螺旋线，并计算长度：ArcLength[{t Cos[t], t Sin[t], 2 t}, {t, 0,12 Pi}]

5、曲面的长度是无限大！但是，对于三维参数方程，却不执行：ArcLength[{Cos[u],Cos[v],Sin[u]},{u,0,2 Pi},{v,0 ,Pi}]