同弧所对的圆周角相等怎么证明

1、使用cad打开我们需要证明的图形，如图所示：

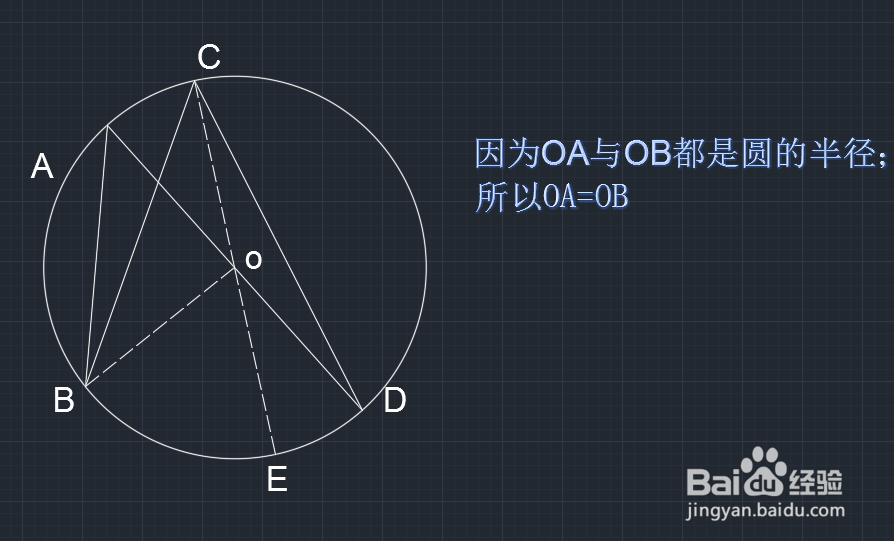
2、打开图形之后我们分别连接圆心做出辅助线，如图所示：

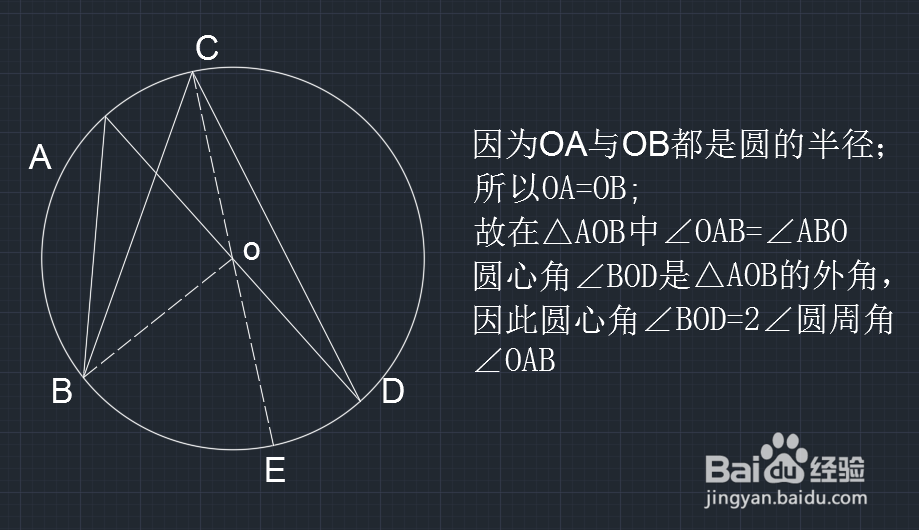
3、做好辅助线之后，在△OAB中，OA与OB都是半径，所以OA=OB，如图所示：

4、由于OA=OB，所以∠OAB=∠OBA，如图所示：

5、∠BOD是是△OAB的外角，所以∠BOD=2∠OAB,如图所示：

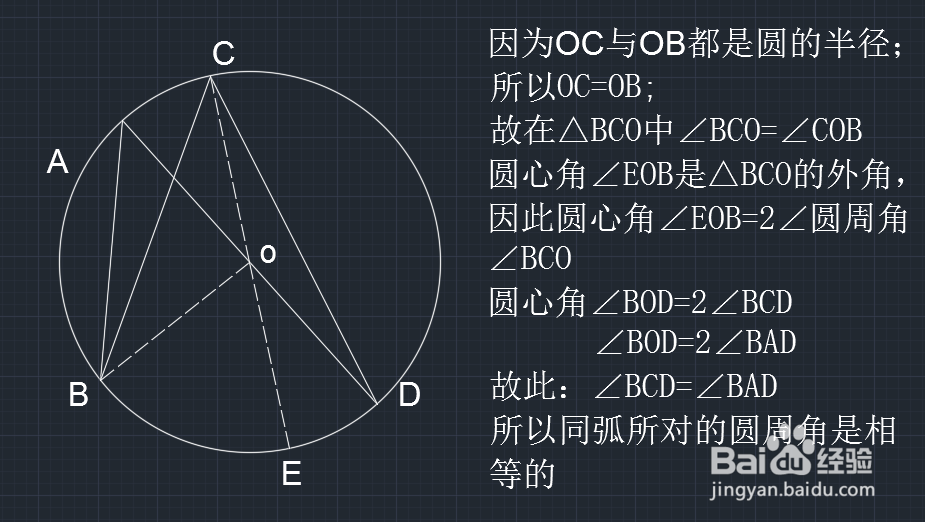
6、在三角形OCD中，OC与OD是半径，所以OC=OD,∠OCD=∠CDO，∠EOD是怅落懊杌△COD的外角，∠EOD=2∠OCD所以如图所示 :

7、在三角形OCB中，OC与OB是半径，所以OC=OB,∠OCB=∠CBO，∠EOB是怅落懊杌△COB的外角，∠EOB=2∠OCB所以如图所示 :

8、故此圆心角∠BOD=2∠BCD，如图所示：

9、由以上步骤可知∠BOD=2∠BCD，∠BOD=2∠BAD,所以∠BCD=∠BAD，故此得出结论同弧所对的圆周角是相等的，如图所示：