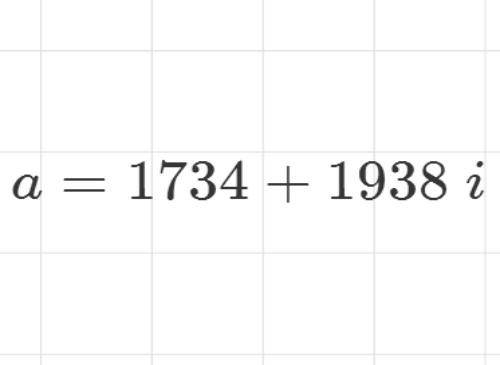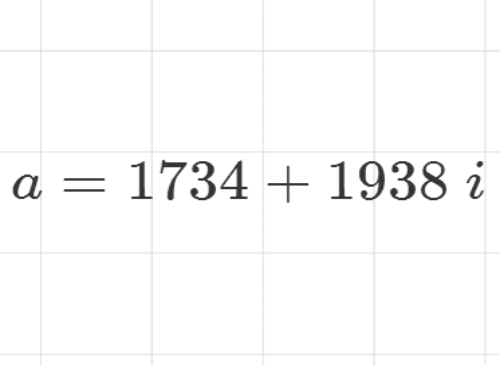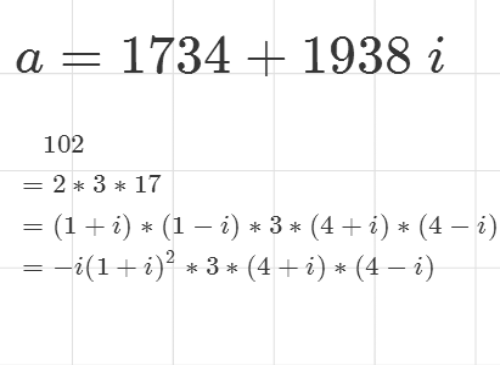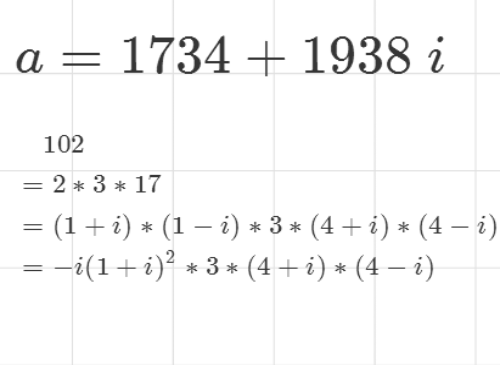【抽象代数】Gauss整数环里面的素因子分解

1、给定一个数字a=1734+1938i。

2、先提取实部和虚部的公因数102。

3、在整数范围内对102进行素因子分解。102=2*3*17其中，3是Gauss素数，而2和17不是Gauss素数，还可以进一步分解。

4、然后再尝试着分解a的复数部分。a=102(17+19i)N(17+19i)=650=2*5*5*13

5、在以前的文章里面，我们证明了，N(ab)=N(a)N(b)，所以:1+i|a；±2莛惧缡笆±3i、±2i±3其中有一个能够整除a；±2±i、±1±2i其中有一个能够整除a。

6、于是，a可以完全分解为Gauss素数的乘积。