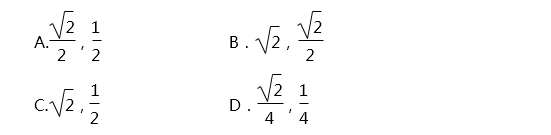高中数学必修二平面解析几何之两直线的位置关系

高中数学必修二平面解析几何重点介绍两直线的位置关系基础知识和易误点，并用平面解析几何两直线3个经典习题和2017年高考试题归纳与整理。

工具/原料

一、 基础知识

平面解析几何之两直线的位置关系辨明三个易误点

三、平面解析几何 经典案例

一、 基础知识

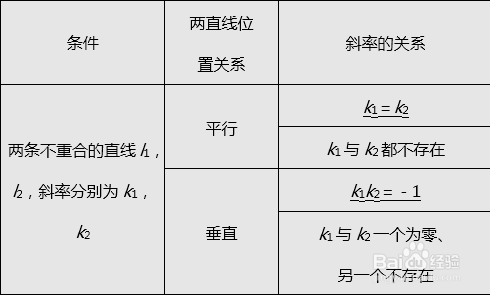
1、两直线的平行、垂直与其斜率的关系

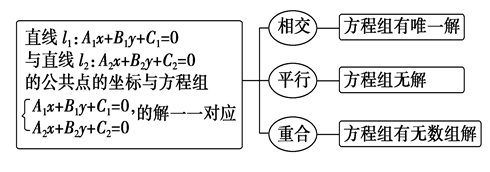
2、2.两条直线的交点

3、3．三种距离

二、平面解析几何之两直线的位置关系辨明三个易误点

1、两条直线平行与垂直

1、(1)设不同直线l1：2x－my－1＝0，l2：(m－1)x－y＋1＝0，则“m＝2”是“l1∥l2”的(　　)A．充分而不必要条件B．必要而不充分条件C．充分必要条件D．既不充分也不必要条件(2)经过两直线l1：x－2y＋4＝0和l2：x＋y－2＝0的交点P，且与直线l3：3x－4y＋5＝0垂直的直线l的方程为________．

2、两条直线平行与垂直解题方法

2、距离公式

2、(1)已知A(2，0)，B(0，2)，若点C在函数y＝x2的图象上，则使得△ABC的面积为2的点C的个数为烫喇霰嘴(　　)A．4　　　　　　　　　　　 B．3C．2 D．1(2)若两平行直线3x－2y－1＝0，6x＋ay＋c＝0之间的距离为，则c的值是________．

3、距离公式解题方法

3、对称问题

1、已知直帧霭绎郎线l：2x－3y＋1＝0，点A(－1，－2)．求：(1)点A关于直线l的对称点A′的坐标；(2)直线m：3x－2y－6＝0关于直线l的对称直线m′的方程；(3)直线l关于点A(－1，－2像粜杵泳)对称的直线l′的方程．

2、对称问题解题方法

3、(2017·南昌模拟)设两条直线的方程分别为x＋y＋a＝0，x＋y＋b＝0，已知a，b是方程x2＋x＋c＝0的两个实根，且0≤c≤，则这两条直线之间的距离的最大值和最小值分别是(　　)