基于MATLAB的音乐合成和处理

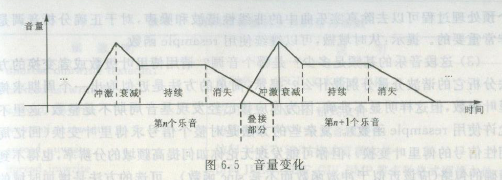
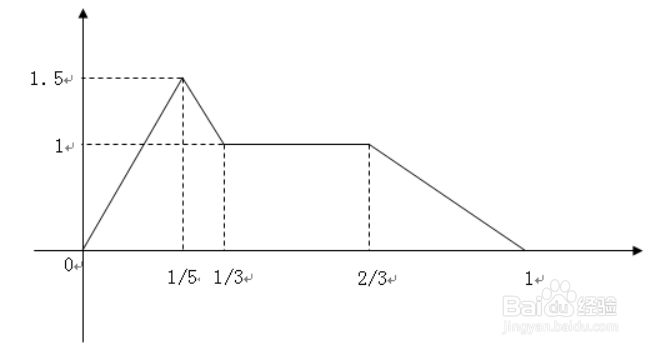
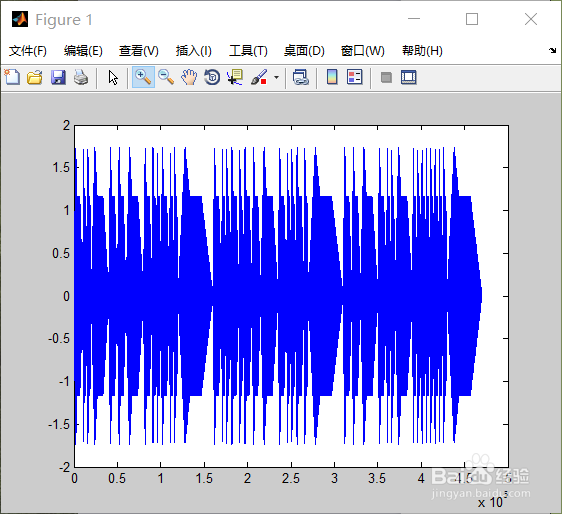
1、基于MATLAB的音乐疙熳阊涓信号合成与处理摘 要本设计共有三部分：1.简单的音乐合成；2.用傅里叶变换分析音乐；3.基于傅里叶级数的音乐合成。本设计采用MATLAB软件仿真来实现。首先,通过对音乐信号的采样、抽取、调制、解调等多种处理过程的理论分析和MATLAB求得这段音乐的基频、谐波分量、等数据;然后,通过对乐理的研究,根据分析中求得的数据编写程序,进行基于傅里叶分析的音乐合成设计，并设计了图形用户界面；最后增强软件编程实现能力和解决实际问题的能力。1简单的合成音乐1.1 乐理知识介绍　　乐音的基本特征可以用基波频率、谐波频谱和包络波形3个方面来描述。基波频率：每个指定音调的唱名都对应固定的基波信号频率。所谓唱名是指平日读乐谱唱出的1(do)、2(re)、3(mi)… … ,每个唱名并未固定基波频率。当指定乐曲的音调时才知道此时唱名对应的频率值。如C调“ 1”的基波频率为261.63HZ,F调“1”的基波频率为349.23HZ,F调“ 5”的基波频率为523.25HZ。谐波频谱:在这七个音符中有一个规律，就是3（mi）到4（fa），7（si）到高音1（do）是半音。在吉他上是相邻的两个品为半音，比如一弦1品是3（mi），那么一弦2品就是4（fa）；在吉他上隔一品是全音，比如一弦1品是1（do），那么一弦3品就是2（re），中间隔了1品。包络波形:不同类型的乐器,包络形状也不相同。在音乐合成实验中,为简化编程描述,通常把复杂的包络函数用少量直线近似。于是,乐音波形的包络呈拆线。有时为了保证在乐音的邻接处信号幅度为零,也可以用指数衰减的包络来表示,这也是最简单的办法。1.2 利用MATLAB实现音乐合成本设计采用扬基杜德尔小曲作根据《扬基杜德尔》第一小节的简谱和十二平均律计算出该小节每个乐音的频率，在MATLAB中生成幅度为1，抽样频率为8kHz的正弦信号表示这些乐音，用sound播放合成的音乐。而在MATLAB中表示乐音所用的抽样频率为fs=8000Hz，也就是所1s钟内有8000个点，抽样点数的多少就可表示出每个乐音的持续时间的长短。用一个行向量来存储这段音乐对应的抽样点，在用sound函数播放即可。下为在MATLAB中编写程序clcclearfs=44100;t=0:1/fs:0.5;c3_2=key(48, 2, fs);d3_2=key(50, 2, fs);e3_2=key(52, 2, fs);f3_2=key(53, 2, fs);g3_2=key(55, 2, fs);a3_2=key(57, 2, fs);b3_2=key(59, 2, fs);c3_4=key(48, 4, fs);d3_4=key(50,4, fs);e3_4=key(52, 4, fs);f3_4=key(53, 4, fs);g3_4=key(55, 4, fs);a3_4=key(57, 4, fs);b3_4=key(59, 4, fs);c3_8=key(48, 8, fs);d3_8=key(50,8, fs);e3_8=key(52, 8, fs);f3_8=key(53, 8, fs);g3_8=key(55, 8, fs);a3_8=key(57, 8, fs);b3_8=key(59, 8, fs);c3_16=key(48, 16, fs);d3_16=key(50,16, fs);e3_16=key(52, 16, fs);f3_16=key(53, 16, fs);g3_16=key(55,16, fs);a3_16=key(57, 16, fs);b3_16=key(59, 16, fs);c4_2=key(60, 2, fs);d4_2=key(62, 2, fs);e4_2=key(64, 2, fs);f4_2=key(65, 2, fs);g4_2=key(67, 2, fs);a4_2=key(69, 2, fs);b4_2=key(71, 2, fs);c4_4=key(60, 4, fs);d4_4=key(62, 4, fs);e4_4=key(64, 4, fs);f4_4=key(65, 4, fs);g4_4=key(67, 4, fs);a4_4=key(69, 4, fs);b4_4=key(71, 4, fs);c4_8=key(60, 8, fs);d4_8=key(62, 8, fs);e4_8=key(64, 8, fs);f4_8=key(65, 8, fs);g4_8=key(67, 8, fs);a4_8=key(69, 8, fs);b4_8=key(71, 8, fs);c4_16=key(60, 16, fs);d4_16=key(62,16, fs);e4_16=key(64, 16, fs);f4_16=key(65, 16, fs);g4_16=key(67, 16, fs);a4_16=key(69, 16, fs);b4_16=key(71, 16, fs);part1=[g3_4 c4_8 c4_8 d4_8 e4_8 c4_8 e4_8 d4_8 b3_8];part2=[c4_8 c4_8 d4_8 e4_8 c4_4 b3_8 g3_8 ];part3=[c4_8 c4_8 d4_8 e4_8 f4_8 e4_8 d4_8 c4_8 b3_8 g3_8 a3_8 b3_8 c4_4 c4_4];part4=[a3_8 b3_16 a3_8 g3_8 a3_8 b3_8 c4_4];part5=[g3_8 a3_16 g3_8 f3_8 e3_8 f3_8 g3_4];part6=[a3_8 b3_16 a3_8 g3_8 a3_8 b3_8 c4_4];part7=[g3_8 c4_8 b3_8 d4_8 c4_4 c4_4];para1=[part1 part2 part3 ];para2=[part4 part5 ];para3=[part6 part7 ];legend=[para1 para2 para3];sound(legend,fs)将该程序在MATLAB中运行，我们可以听出音色一般，需要改进。1.2除噪音，加包络下面通过加包络来消噪音。最简单的包络为指数衰减。最简单的指数衰减是对每个音乘以因子，在实验中首先加的是的衰减，这种衰减方法使用的是相同速度的衰减，但是发现噪音并没有完全消除，播放的音乐效果不是很好，感觉音乐起伏性不强。于是采用不同速度的衰减，根据乐音持续时间的长短来确定衰减的快慢，乐音持续时间越长，衰减的越慢，持续时间越短，衰减的越快。更科学的包络如下图所示，每个乐音都经过冲激、衰减、持续、消失四个阶段。由上图可以看出这个包络是四段直线段构成的，因此只要确定了每段线段的端点，即可用端点数据写出直线方程，因为直线方程可以用通式写出（我用的是斜截式），因此这段包络可以用简单的循环来完成。例如认为包络线上的数据如下图所示：据此在MATLAB中编写如下程序：clear;clc;fs=8000; %抽样频率part1=[fre(55) fre(60) fre(60) fre(62) fre(64) fre(60) fre(64) fre(62) fre(59)];part2=[fre(60) fre(60) fre(62) fre(64) fre(60) fre(59) fre(55)];part3=[fre(60) fre(60) fre(62) fre(64) fre(65) fre(64) fre(62) fre(60) fre(59) fre(55) fre(57) fre(59) fre(60) fre(60)];part4=[fre(57) fre(59) fre(57) fre(55) fre(57) fre(59) fre(60)];part5=[fre(55) fre(57) fre(55) fre(53) fre(52) fre(53) fre(55)];part6=[fre(57) fre(59) fre(57) fre(55) fre(57) fre(59) fre(60)];part7=[fre(55) fre(60) fre(59) fre(62) fre(60) fre(60)];para1=[part1 part2 part3 ];para2=[part4 part5 ];para3=[part6 part7 ];f=[para1 para2 para3]; %各个乐音对应的频率part1time=[0.5 0.25 0.25 0.25 0.25 0.25 0.25 0.25 0.25];part2time=[0.25 0.25 0.25 0.25 0.5 0.25 0.25];part3time=[0.25 0.25 0.25 0.25 0.25 0.25 0.25 0.25 0.25 0.25 0.25 0.25 0.5 0.5];part4time=[0.25 0.125 0.25 0.25 0.25 0.25 0.5];part5time=[0.25 0.125 0.25 0.25 0.25 0.25 0.5];part6time=[0.25 0.125 0.25 0.25 0.25 0.25 0.5];part7time=[0.25 0.25 0.25 0.25 0.5 0.5];para1time=[part1time part2time part3time ];para2time=[part4time part5time ];para3time=[part6time part7time ];time=fs*[para1time para2time para3time];%各个乐音的抽样点数N=length(time); %这段音乐的总抽样点数east=zeros(1,N); %用east向量来储存抽样点n=1;for num=1:N %利用循环产生抽样数据，num表示乐音编号t=1/fs:1/fs:time(num)/fs; %产生第num个乐音的抽样点baoluo=zeros(1,time(num)); %P为存储包络数据的向量for j=1:time(num)if(j<0.2*time(num))y=7.5*j/time(num);elseif(j<0.333*time(num))y=-15/4*j/time(num)+9/4;elseif(j<0.666*time(num))y=1;elsey=-3*j/time(num)+3;endendendbaoluo(j)=y;endeast(n:n+time(num)-1)=sin(2*pi*f(num)*t).*baoluo(1:time(num));%给第num个乐音加上包络n=n+time(num);endsound(east,8000) %播放音乐plot(east)此处利用函数frefunction f = fre(p)f=440*2^((p-69)/12);运行得到的图像为：下图是两个乐音交接处的局部放大图，可以看到知道前一个乐音衰减到零时，后一个乐音才开始从零增加，所以可以说消除了噪音。1.3改编程序，实现1.2中乐曲的升八度升高一个八度就是将每个乐音的频率都提高一倍，变为原来的2倍；降低一个八度即每个乐音的频率都减小一倍，变为原来的1/2。因此将存储乐音频率的向量每个元素改变为2或1/2倍即可。查表得到下列MATLAB程序clcclearfs=44100;t=0:1/fs:0.5;c4_2=key(60, 2, fs);d4_2=key(62, 2, fs);e4_2=key(64, 2, fs);f4_2=key(65, 2, fs);g4_2=key(67, 2, fs);a4_2=key(69, 2, fs);b4_2=key(71, 2, fs);c4_4=key(60, 4, fs);d4_4=key(62, 4, fs);e4_4=key(64, 4, fs);f4_4=key(65, 4, fs);g4_4=key(67, 4, fs);a4_4=key(69, 4, fs);b4_4=key(71, 4, fs);c4_8=key(60, 8, fs);d4_8=key(62, 8, fs);e4_8=key(64, 8, fs);f4_8=key(65, 8, fs);g4_8=key(67, 8, fs);a4_8=key(69, 8, fs);b4_8=key(71, 8, fs);c4_16=key(60, 16, fs);d4_16=key(62,16, fs);e4_16=key(64, 16, fs);f4_16=key(65, 16, fs);g4_16=key(67, 16, fs);a4_16=key(69, 16, fs);b4_16=key(71, 16, fs);c5_2=key(72, 2, fs);d5_2=key(74, 2, fs);e5_2=key(76, 2, fs);f5_2=key(77, 2, fs);g5_2=key(79, 2, fs);a5_2=key(81, 2, fs);b5_2=key(83, 2, fs);c5_4=key(72, 4, fs);d5_4=key(74, 4, fs);e5_4=key(76, 4, fs);f5_4=key(77, 4, fs);g5_4=key(79, 4, fs);a5_4=key(81, 4, fs);b5_4=key(83, 4, fs);c5_8=key(72, 8, fs);d5_8=key(74, 8, fs);e5_8=key(76, 8, fs);f5_8=key(77, 8, fs);g5_8=key(79, 8, fs);a5_8=key(81, 8, fs);b5_8=key(83, 8, fs);c5_16=key(72, 16, fs);d5_16=key(74,16, fs);e5_16=key(76, 16, fs);f5_16=key(77, 16, fs);g5_16=key(79, 16, fs);a5_16=key(81, 16, fs);b5_16=key(83, 16, fs);part1=[g4_4 c5_8 c5_8 d5_8 e5_8 c5_8 e5_8 d5_8 b4_8];part2=[c5_8 c5_8 d5_8 e5_8 c5_4 b4_8 g4_8 ];part3=[c5_8 c5_8 d5_8 e5_8 f5_8 e5_8 d5_8 c5_8 b4_8 g4_8 a4_8 b4_8 c5_4 c5_4];part4=[a4_8 b4_16 a4_8 g4_8 a4_8 b4_8 c5_4];part5=[g4_8 a4_16 g4_8 f4_8 e4_8 f4_8 g4_4];part6=[a4_8 b4_16 a4_8 g4_8 a4_8 b4_8 c5_4];part7=[g4_8 c5_8 b4_8 d5_8 c5_4 c5_4];para1=[part1 part2 part3 ];para2=[part4 part5 ];para3=[part6 part7 ];legend=[para1 para2 para3];sound(legend,fs)1.4在1.2的音乐中加入谐波我们在1.2的音乐中分别加上二、三、四次谐波，其基波幅度为1，高次谐波幅度分别为0.2、0.3、0.1。应该将程序改为：clear;clc;fs=8000; %抽样频率part1=[fre(55) fre(60) fre(60) fre(62) fre(64) fre(60) fre(64) fre(62) fre(59)];part2=[fre(60) fre(60) fre(62) fre(64) fre(60) fre(59) fre(55)];part3=[fre(60) fre(60) fre(62) fre(64) fre(65) fre(64) fre(62) fre(60) fre(59) fre(55) fre(57) fre(59) fre(60) fre(60)];part4=[fre(57) fre(59) fre(57) fre(55) fre(57) fre(59) fre(60)];part5=[fre(55) fre(57) fre(55) fre(53) fre(52) fre(53) fre(55)];part6=[fre(57) fre(59) fre(57) fre(55) fre(57) fre(59) fre(60)];part7=[fre(55) fre(60) fre(59) fre(62) fre(60) fre(60)];para1=[part1 part2 part3 ];para2=[part4 part5 ];para3=[part6 part7 ];f=[para1 para2 para3]; %各个乐音对应的频率part1time=[0.5 0.25 0.25 0.25 0.25 0.25 0.25 0.25 0.25];part2time=[0.25 0.25 0.25 0.25 0.5 0.25 0.25];part3time=[0.25 0.25 0.25 0.25 0.25 0.25 0.25 0.25 0.25 0.25 0.25 0.25 0.5 0.5];part4time=[0.25 0.125 0.25 0.25 0.25 0.25 0.5];part5time=[0.25 0.125 0.25 0.25 0.25 0.25 0.5];part6time=[0.25 0.125 0.25 0.25 0.25 0.25 0.5];part7time=[0.25 0.25 0.25 0.25 0.5 0.5];para1time=[part1time part2time part3time ];para2time=[part4time part5time ];para3time=[part6time part7time ];time=fs*[para1time para2time para3time];%各个乐音的抽样点数N=length(time); %这段音乐的总抽样点数east=zeros(1,N); %用east向量来储存抽样点n=1;for num=1:N %利用循环产生抽样数据，num表示乐音编号t=1/fs:1/fs:time(num)/fs; %产生第num个乐音的抽样点baoluo=zeros(1,time(num)); %P为存储包络数据的向量for j=1:time(num)if(j<0.2*time(num))y=7.5*j/time(num);elseif(j<0.333*time(num))y=-15/4*j/time(num)+9/4;elseif(j<0.666*time(num))y=1;elsey=-3*j/time(num)+3;endendendbaoluo(j)=y;endh=[1 0.2 0.3 0.1];xiebo=zeros(1,length(t));for i=1:length(n)xiebo=xiebo+h(i)*sin(2*i*pi*f(num)*t);endeast(n:n+time(num)-1)=xiebo.*baoluo(1:time(num));n=n+time(num);endsound(east,8000) %播放音乐plot(east) %图像加入谐波后音色得到明显好转运行得到的图像为：

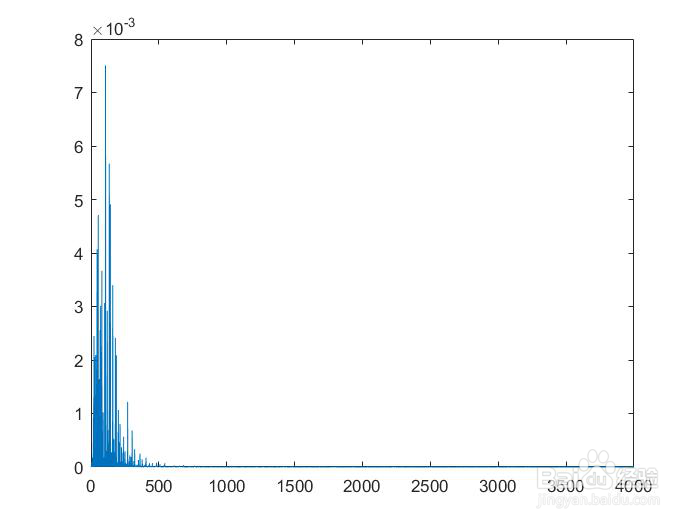
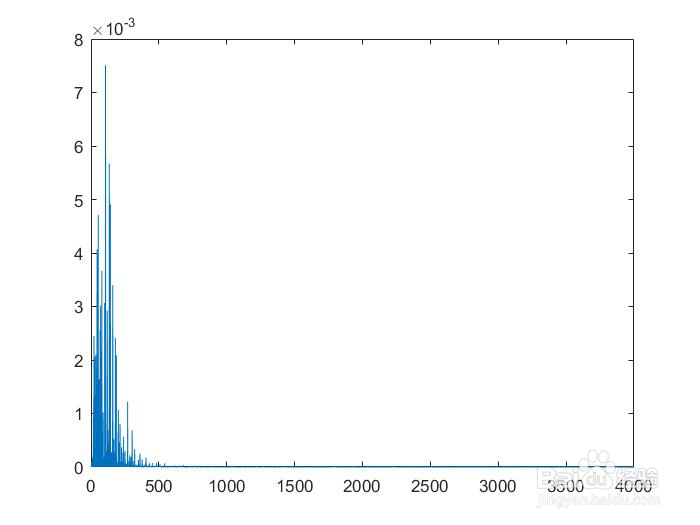
2、2.用傅里叶变换分析音乐2.1 分析can.wav的音调和节拍我们对can进行傅里叶变换分析其基波和谐波，得到can的幅值谱，频谱图上的第一个突出的波峰对应的频率即为can的基频，可编写了如下程序：clear;clc;[y,Fs]= audioread('can.wav');fs=8000;NFFT = 2^nextpow2(length(y));Y = fft(y,NFFT)/length(y);g = fs/2*linspace(0,1,NFFT/2+1);plot(g,2*abs(Y(1:NFFT/2+1)))运行后得到的结果为通过增加can的周期性显示出离散化程度高的幅值谱，即让can在时域重复多次后在进行傅里叶变换。利用repmat函数将can在时域内重复。程序可修改为:clear;clc;WAV= audioread('can.wav');fs=8000;wave2proc =repmat(WAV,20,1); %将 can重复20次NFFT = 2^nextpow2(length(WAV));Y = fft(WAV,NFFT)/length(WAV);g = fs/2*linspace(0,1,NFFT/2+1);plot(g,2*abs(Y(1:NFFT/2+1)))由图读出can的基频为329.1Hz，幅值为2.451，高次谐波幅值分别为：2.2 根据快速傅里叶变换合成音乐将程序中的波形幅度矩阵m=[1 0.3 0.2 0.1]改为m=[2.0912 4.0597 4.7156 7.5215 5.6484 4.9845 3.4894 2.4568];即可程序如下clear;clc;fs=8000; %抽样频率part1=[fre(67) fre(72) fre(72) fre(74) fre(76) fre(72) fre(76) fre(74) fre(71)];part2=[fre(72) fre(72) fre(74) fre(76) fre(72) fre(71) fre(67)];part3=[fre(72) fre(72) fre(74) fre(76) fre(77) fre(76) fre(74) fre(72) fre(71) fre(67) fre(69) fre(71) fre(72) fre(72)];part4=[fre(69) fre(71) fre(69) fre(67) fre(69) fre(71) fre(72)];part5=[fre(67) fre(69) fre(67) fre(65) fre(64) fre(65) fre(67)];part6=[fre(69) fre(71) fre(69) fre(67) fre(69) fre(71) fre(72)];part7=[fre(67) fre(72) fre(71) fre(74) fre(72) fre(72)];para1=[part1 part2 part3 ];para2=[part4 part5 ];para3=[part6 part7 ];f=[para1 para2 para3]; %各个乐音对应的频率part1time=[0.5 0.25 0.25 0.25 0.25 0.25 0.25 0.25 0.25];part2time=[0.25 0.25 0.25 0.25 0.5 0.25 0.25];part3time=[0.25 0.25 0.25 0.25 0.25 0.25 0.25 0.25 0.25 0.25 0.25 0.25 0.5 0.5];part4time=[0.25 0.125 0.25 0.25 0.25 0.25 0.5];part5time=[0.25 0.125 0.25 0.25 0.25 0.25 0.5];part6time=[0.25 0.125 0.25 0.25 0.25 0.25 0.5];part7time=[0.25 0.25 0.25 0.25 0.5 0.5];para1time=[part1time part2time part3time ];para2time=[part4time part5time ];para3time=[part6time part7time ];time=fs*[para1time para2time para3time];%各个乐音的抽样点数N=length(time); %这段音乐的总抽样点数east=zeros(1,N); %用east向量来储存抽样点n=1;for num=1:N %利用循环产生抽样数据，num表示乐音编号t=1/fs:1/fs:time(num)/fs; %产生第num个乐音的抽样点baoluo=zeros(1,time(num)); %P为存储包络数据的向量for j=1:time(num)if(j<0.2*time(num))y=7.5*j/time(num);elseif(j<0.333*time(num))y=-15/4*j/time(num)+9/4;elseif(j<0.666*time(num))y=1;elsey=-3*j/time(num)+3;endendendbaoluo(j)=y;endh=[2.0912 4.0597 4.7156 7.5215 5.6484 4.9845 3.4894 2.4568];xiebo=zeros(1,length(t));for i=1:length(n)xiebo=xiebo+h(i)*sin(2*i*pi*f(num)*t);endeast(n:n+time(num)-1)=xiebo.*baoluo(1:time(num));n=n+time(num);endsound(east,8000) %播放音乐plot(east) %图像

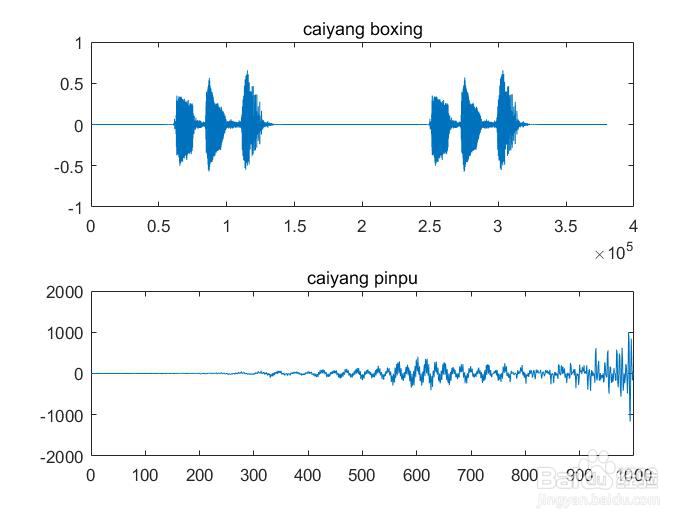
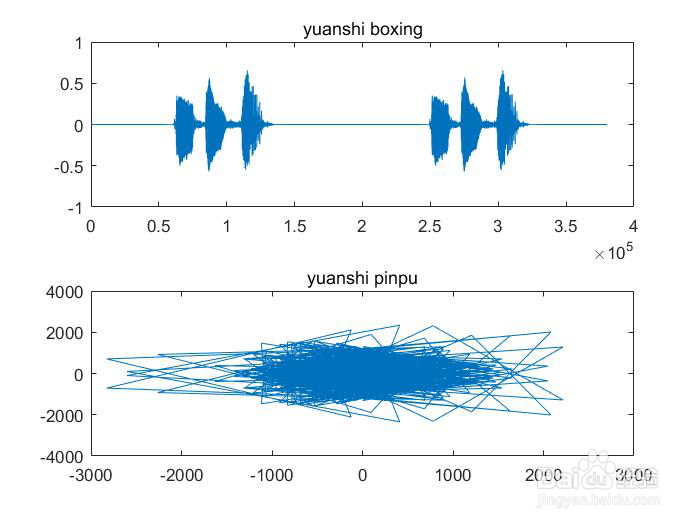
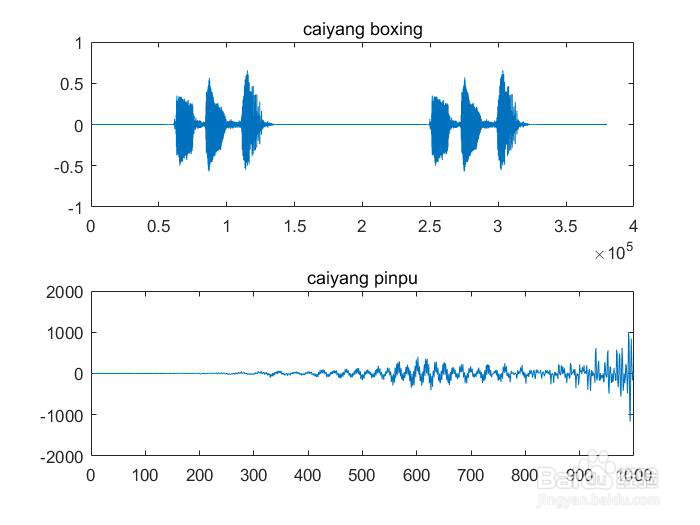
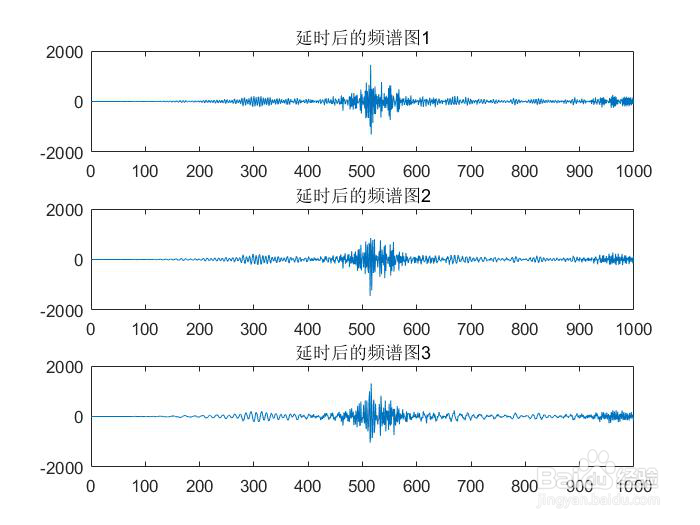
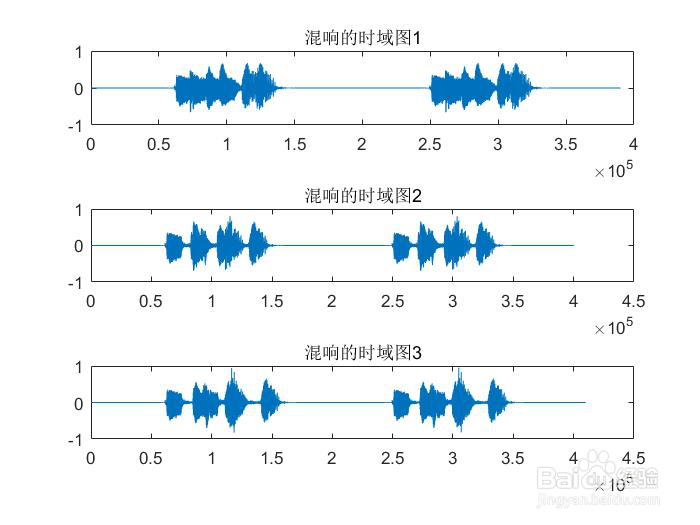
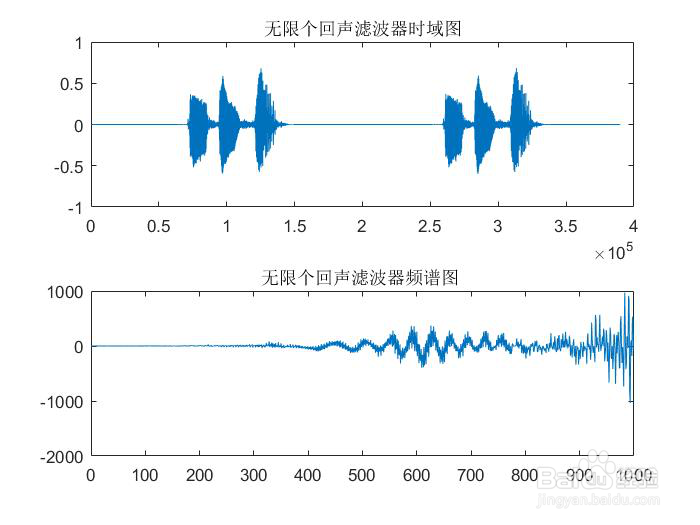
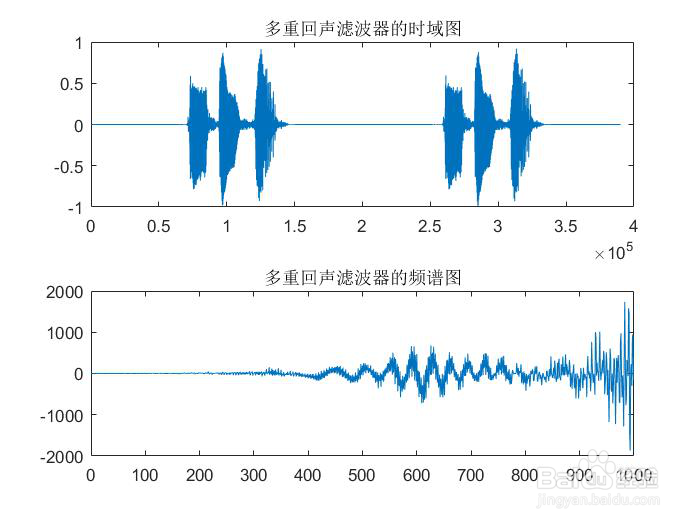
3、第三部分 音乐信号的处理3.1加入延时和混响选择一段语音信号作为分析对象，并对其进行频谱分镙龟陛鹜析，在时域中用数字信号处理方法给信号加入泌驾台佐3种混响，再分析其频谱，并与原始信号进行比较。设计思路1、利用Windows下的录音机或其他软件，录制一段语音信号，时间控制在3s左右，并对录制的信号进行采样2、语音信号的频谱分析，画出采样后的时域波形和频谱图3、将信号加入延时和混响，再分析其时域波形和频谱图，并与原始信号频谱进行比较所以根据设计思路进行实验1、读取3s的语音信号并画出时域波形和频谱图x1=audioread('good.wav');[x,fs]=audioread('good.wav');x=x(:,1); %取单声道sound(x,fs);X=fft(x,640000); %gaidongmagX=abs(X);angX=angle(X);figure(1);subplot(2,1,1);plot(x);title('yuanshi boxing');subplot(2,1,2);plot(X);title('yuanshi pinpu');得到的波形和频谱图为2、对语音信号进行采样并画出采样后信号的时域波和频谱图[x,fs]=audioread('good.wav');x=x(:,1);sound(5*x,fs);n1=0:2000;N=size(x,1);Y=fft(x,320000);figure(2);subplot(2,1,1);plot(x);title('caiyang boxing');subplot(2,1,2);plot(n1(1:1000),Y(1:1000));title('caiyang pinpu');得到的采样波形和频谱为3、对采样后的信号延时，并画出延时后的时域波形和频谱图z1=[zeros(10000,1);x]; %对信号进行延时z2=[zeros(20000,1);x];z3=[zeros(30000,1);x];Z1=fft(z1,160000);Z2=fft(z2,160000);Z3=fft(z3,160000);figure(3); subplot(3,1,1);plot(z1); title('延时后的时域图1'); %画出延时后的信号时域图subplot(3,1,2);plot(z2); title('延时后的时域图2');subplot(3,1,3);plot(z3); title('延时后的时域图3');figure(4)subplot(3,1,1);plot(n1(1:1000),Z1(1:1000));title('延时后的频谱图1'); %延时后的信号频谱图subplot(3,1,2);plot(n1(1:1000),Z2(1:1000));title('延时后的频谱图2'); subplot(3,1,3);plot(n1(1:1000),Z3(1:1000));title('延时后的频谱图3');得到延时的时域图和频谱图为4、对信号进行混响，并画出混响后的时域波形和频谱图z1=[zeros(10000,1);x]; %对信号进行延时z2=[zeros(20000,1);x];z3=[zeros(30000,1);x];x1=[x;zeros(10000,1)]; %使语音信号与延时后信号同等长度x2=[x;zeros(20000,1)];x3=[x;zeros(30000,1)];y1=plus(x1,z1); %信号的混响y2=plus(x2,z2);y3=plus(x3,z3);sound(y1,fs);sound(y2,fs);sound(y3,fs);figure(5);subplot(3,1,1);plot(y1); title('混响的时域图1'); %混响时域图subplot(3,1,2);plot(y2); title('混响的时域图2');subplot(3,1,3);plot(y3); title('混响的时域图3');Y1=fft(y1,160000); %对混响信号FFT变换Y2=fft(y2,160000);Y3=fft(y3,160000);figure(6);subplot(3,1,1);plot(n1(1:1000),Y1(1:1000)); title('混响的频谱图1'); %混响频谱图subplot(3,1,2);plot(n1(1:1000),Y2(1:1000)); title('混响的频谱图2');subplot(3,1,3);plot(n1(1:1000),Y3(1:1000)); title('混响的频谱图3');得到的混响后的时域波形和频谱图为3.2均衡处理设计思路：设计三个混响器作为均衡处理的工具（1）无限回声混响器a=0.05; %a取小于等于1Bz=[0,0,0,0,0,0,0,0,0,0,1]; %分子的系数Az=[1,0,0,0,0,0,0,0,0,0,-a]; %分母的系数yy1=filter(Bz,Az,z1); %滤波器进行滤波YY1=fft(yy1,320000); %经无限回声滤波器后的信号做32000点的FFT变换（2）多重回声混响器a=0.05; %a取小于等于1N=5Bz1=[1,0,0,0,0,0,0,0,0,0,-0.5^N] %分子的系数Az1=[1,0,0,0,0,0,0,0,0,0,-0.5]; %分母的系数yy2=filter(Bz1,Az1,z1); %滤波器进行滤波YY2=fft(yy2,320000); %经多重回声滤波器后的信号做32000点的FFT变换（3）全通结构的混响器a=0.05; %a取小于等于1Bz1=[a,0,0,0,0,0,0,0,0,0,1]; %分子的系数Az1=[1,0,0,0,0,0,0,0,0,0,a]; %分母的系数yy3=filter(Bz1,Az1,z1); %滤波器进行滤波YY3=fft(yy3,320000); %经全通结构的混响器后的信号做32000点的FFT变最后输出声音sound(yy1,fs);sound(yy2,fs);sound(yy3,fs);（4）画出经混响器处理后信号的时域波形和频谱图figure(8);subplot(2,1,1);plot(yy1);title('无限个回声滤波器时域图'); %无限回声滤波器时域波形subplot(2,1,2);plot(n1(1:1000),YY1(1:1000));title('无限个回声滤波器频谱图 '); %无限回声滤波器频谱图figure(9)subplot(2,1,1);plot(yy2);title('多重回声滤波器的时域图') %多重回声滤波器的混响器时域波形subplot(2,1,2);plot(n1(1:1000),YY2(1:1000));title('多重回声滤波器的频谱图') %多重回声滤波器的频谱图figure(10)subplot(2,1,1);plot(yy3);title('全通结构滤波器的时域图') %全通结构的混响器时域波形subplot(2,1,2);plot(n1(1:1000),YY3(1:1000));title('全通结构滤波器的频谱图') %全通结构的混响器频谱图得到的波形为