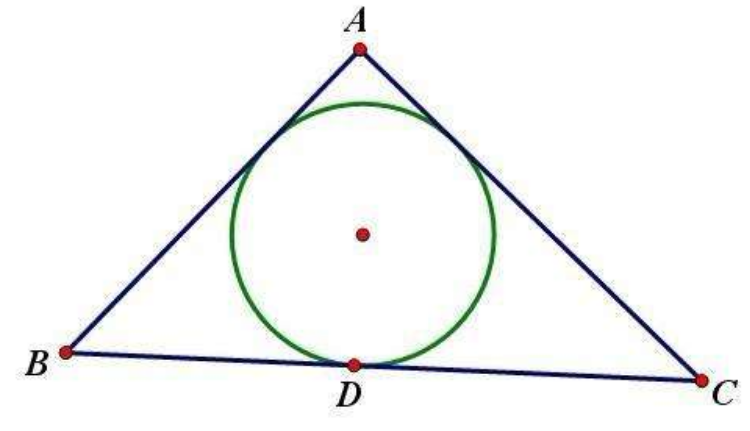
内心是什么的交点

内心是三角形内切圆的圆心，也就是三角形三个角地平分线的交点，它到三角形三边的距离相等。外心是三角形外接圆的圆心，也就是三角形三条边的垂直平分线的交点。

知识拓展

设△ABC的内切圆为☉I(r)，∠A、∠B、∠C的对边分别为a、b、c，p=(a+b+c)/2。

1、三角形的内心到三边的距离相等，都等于内切圆半径r。

2、∠BIC=90°+∠BAC/2。

3、在RtΔABC中，∠A=90°，三角形内切圆切BC于D，则S△ABC=BD×CD。

4、(欧拉定理)△ABC中，R和r分别为外接圆为和内切圆的半径，外心和内心的距离为d，则d²=R^2-2Rr。

5、△ABC中：a，b，c分别为三边，S为三角形面积，则内切圆半径r=2S/(a+b+c)。

6、双曲线上任一支上一点与两焦点组成的三角形的内心在实轴的射影为对应支的顶点。

7、△ABC中，内切圆分别与AB，BC，CA相切于P，Q，R，则AP=AR=(b+c-a)/2， BP =BQ =(a+c-b)/2，CR =CQ =(b+a-c)/2，r=[(b+c-a)tan(A/2)]/2。

8、三角形内角平分线定理：△ABC中，I为内心，∠BAC 、∠ABC、 ∠ACB的内角平分线分别交BC、AC、AB于A'、B'、C'，则BA'/CA'=AB/AC，AB'/CB'=BA/BC，AC'/BC'=CA/CB。

一、三角形的外心和外心的性质

1、“外心”是三角形的垂直平分线的交点，也是三角形外接圆的圆心。垂直平分线也叫“中垂线”。

2、外心性质

（1）三角形的任意一条边的中点和外心的连线必定在这条边的垂直平线上，所以也必定垂直平分这条边。

（2）外心到三角形三个顶点的距离相等，而且都等于这个三角形的外接圆的半径长。

二、三角形的重心和重心的性质

1、“重心”是三角形中线的交点。

2、重心性质

（1）三角形顶点与重心的连线必定在三角形的一条中线上。

（2）延长三角形的一个顶点与重心的连线，使得交于这个顶点的对边上一点，则这个交点为边上的中点。

（3）三角形的重心把三角形的任意一条中线分成两条线段，其中重心到三角形顶点的线段长是另一条线段长的2倍。

三、三角形的垂心和垂心的性质

1、垂心是三角形高线的交点。

2、垂心性质

（1）三角形的顶点与垂心的连线必定在三角形的一条高线上。

（2）三角形任何一个顶点和垂心的连线必定垂直于这个顶点的对边。

四、三角形的中心和中心的性质

1、三角形的“四心”（内心、外心、重心、垂心）重合后的点称为这个三角形的中心。只有等边三角形才有中心。

2、中心性质

因为中心是三角形的内心、外心、重心、垂心“四心”重合后的点，所以等边三角形的中心具有三角形内心、外心、重心、垂心所具有的全部性质。