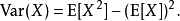数学期望的性质有哪些

数学期望的性质：

1、设X是随机变量，C是常数，则E（CX）=CE（X）。

2、设X，Y是任意两个随机变量，则有E（X+Y）=E（X）+E（Y）。

3、设X，Y是相互独立的随机变量，则有E（XY）=E（X）E（Y）。

4、设C为常数，则E（C）=C。

扩展资料：

期望的应用

1、在统计学中，想要估算变量的期望值时，用到的方法是重复测量此变量的值，然后用所得数据的平均值来作为此变量的期望值的估计。

2、在概率分布中，数学期望值和方差或标准差是一种分布的重要特征。

3、在古典力学中，物体重心的算法与期望值的算法近似，期望值也可以通过方差计算公式来计算方差：

4、实际生活中，赌博是数学期望值的一种常见应用。

参考资料来源：百度百科-数学期望