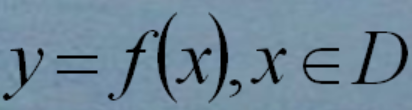二次函数最值问题进一步讨论

1、求定义域。如：f(X)=2x^2-ax+1定义域为【-1,3】

2、求对称轴方程。如：f(X)=2x^2-ax+1对称轴方程为x=a/4

3、求单调区间。如：f(X)=2x^2-ax+1中在（-∞，a/4)单调递减，在（a/4,+∞）单调递增

4、分区间讨论。如f(X)=2x^2-ax+1中（见下一步骤）

5、当a/4≤-1时函数在定义域内单调递增因此在左端点取得最小值，右端点取得最大值

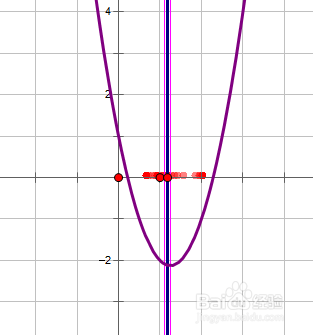
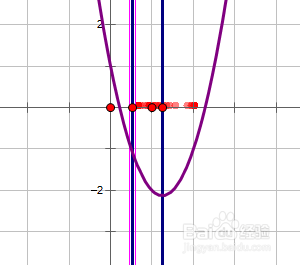
6、当a/4≥3时函数在定义域内单调递减因此在左端点取得最大值，右端点取得最小值

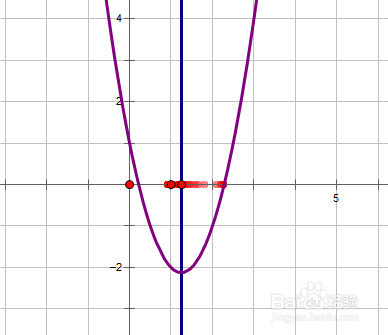
7、当-1<a/4<3时函数在定凶及淄靥义域内既有单调减区间又有单调增区间，因此在对称轴处取得最小，再离对称轴最远处取得最大值

8、综上所述，得出答案。