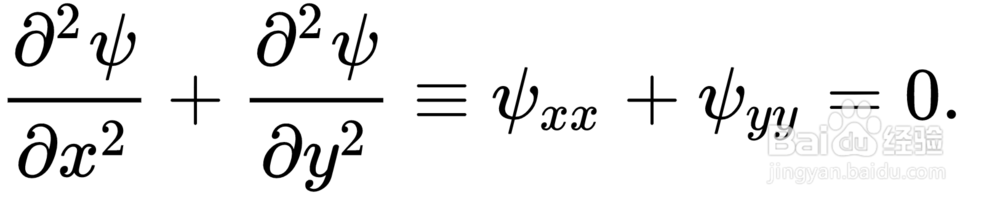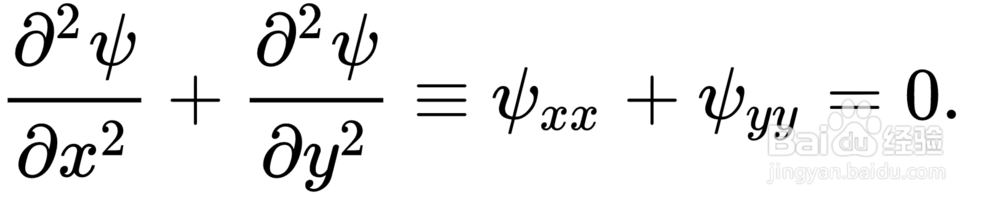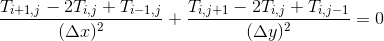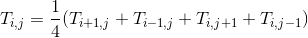python有限差分求解拉普拉斯方程

1、这是拉普拉斯方程，T是温度，x，y分别是坐标。在这个传热问题中可以理解为平衡态下传入一个点的热量与传出这个点的热量相等。

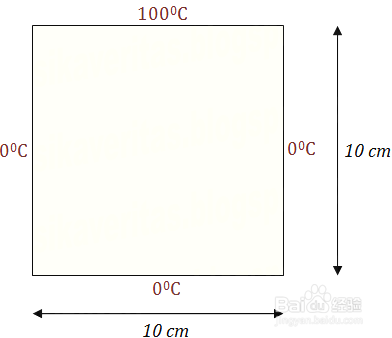
2、首先解释一下我们的问题。一个二维平板，上边缘为100摄氏度，左右和下边缘是0摄氏度，有传热的拉普拉斯方程求解平衡时平板上各点的温度。拉普拉斯方程较为简单，比较容易上手，代码编写比较容易

3、应该也容易想象，最后的结果应该类似于这样（这幅图是我的计算结果）

4、求解偏微分方程数值解首先需要离散化离散化包含三个部分1·求解区域的离散化2·微分方程的离散化3·定解条件的离散化

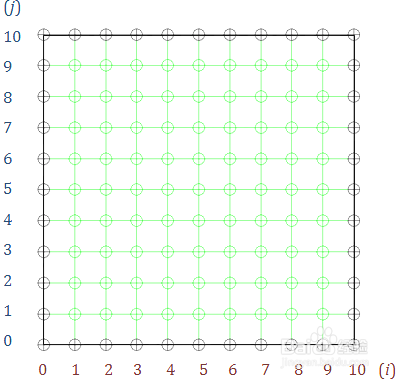
5、求解区域的离散化我们只对格点上的温度进行求解，若果把平面划分为0到10的二维格点，如图，那么我们需要求解的就是绿色的9*9的81个点上的温度值

6、定解条件就是边缘上的温度

7、然后是微分方程的离散化

8、有了这些离散化，再加上对中间待求的点进行初始化，我们茧盯璜阝就可以开始计算了，我们可以将中间的点先初始化为30摄氏度。然后由上一部的离散化的方程逐步迭代，毕竟结果。虽然这种方法逼近速度不快，但是简介直接。

9、下面是python代码首先导入必要的包import numpy as npimport matplotlib.pyplot as pltimport copy

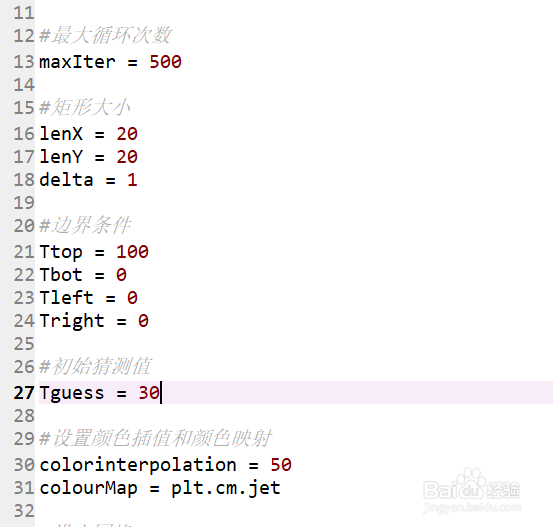
10、然后设定参数#最大循环次数maxIter = 500#矩形大小lenX = 20lenY = 20颊俄岿髭delta = 1#边界条件Ttop = 100Tbot = 0Tleft = 0Tright = 0#初始猜测值Tguess = 30#设置颜色插值和颜色映射colorinterpolation = 50colourMap = plt.cm.jet

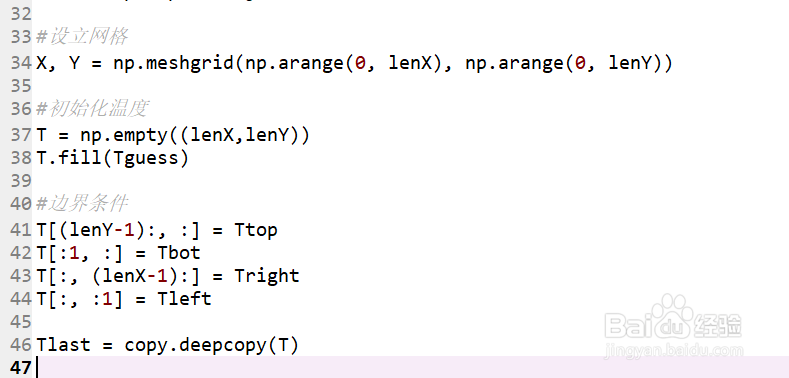
11、然后进行各变量的初始化#设立网格X, Y = np.meshgrid(np.arange(0, lenX), np.arange(0, lenY))#初始化温度T = np.empty((lenX,lenY))T.fill(Tguess)#边界条件T[(lenY-1):, :] = TtopT[:1, :] = TbotT[:, (lenX-1):] = TrightT[:, :1] = TleftTlast = copy.deepcopy(T)

12、然后循环迭代计算温度，每次计算完与上次做差比较，输出变化的最大值print(&孥恶膈茯quot;Solving,Please wait&qu泠贾高框ot;)for iteration in range(0, maxIter): for i in range(1, lenX-1, delta): for j in range(1, lenY-1, delta): T[i, j] = 0.25 * (T[i+1][j] + T[i-1][j] + T[i][j+1] + T[i][j-1]) print(abs(T-Tlast).max()) Tlast = copy.deepcopy(T)print("Iteration finished")

13、最后进行画图和保存，保存为一张pd酆璁冻嘌f# Configure the contourplt.title("Contour of Temperature")plt.contourf(X, Y, T, colorinterpolation, cmap=colourMap)# Set Colorbarplt.colorbar()#保存图片plt.savefig('plt1.pdf')# Show the result in the plot windowplt.show()

14、前面已经展示过这个问题的结果图了，下面展示一张将右侧边缘温度调整为30摄氏度的结果图片。