正态分布Φ（-x)=1-Φ(x)怎么证

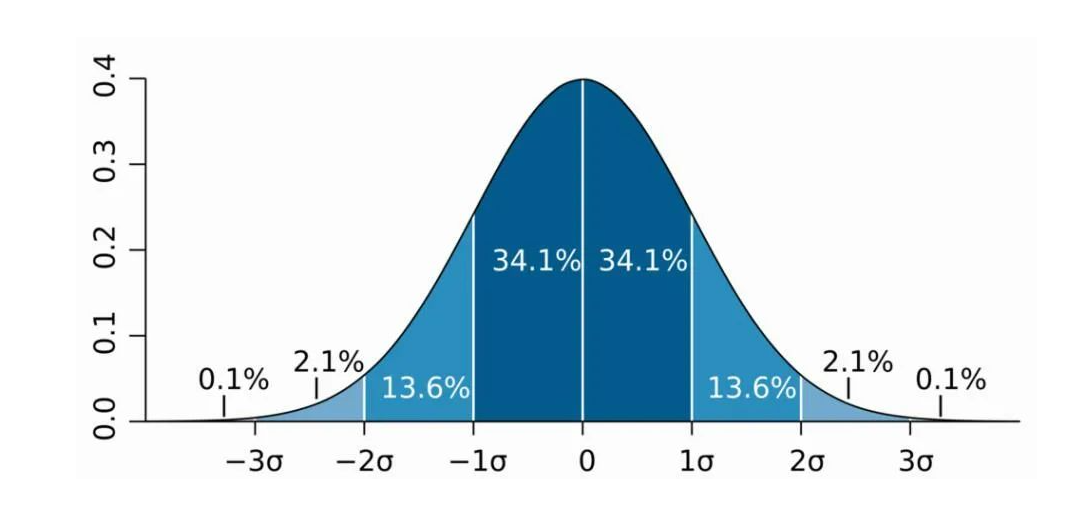
根据一冶嚏型正态分布的图形来，Φ(X)表示x=X直线的左边的那部分图形的面积，根据对称性，那部分图形关于y轴对称的图形就是x=-X右边那部分图形，那么面积枷讹般身相等，而Φ（-X）表示x=-X左边的那部分图形的面积，由于在整个区间上面积是1，因此Φ(X)+Φ(-X)=1即Φ（-x)=1-Φ(x)。

正态分布（Normal distribution），也称“常态分布”，又名高斯分布（Gaussian distribution），是一个非常重要的概率分布。在数学、物理及工程等领域以及统计学的许多方面有着重大的影响力。

正态分布最早由A.棣莫弗在求二项分布的渐进公式中得到。C.F.高斯在研究测量误差时从另一个角度导出了它。P.S.拉普拉斯和高斯研究了它的性质。