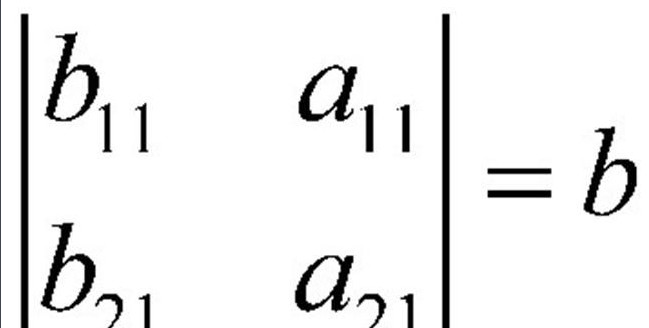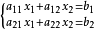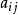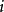已知三点坐标,求围成的三角形面积的一个公式

这是已知三角形3顶点沪蝠喵杰坐标A(x1,y1)，B(x2,y2)，C(x3,y3)，求三角形ABC的面积的公式

公式中书写形式是二阶行列式

写成一般形式如下:

设A(x1,y1)，B(x2,y2)，C(x3,y3)在坐标系中中顺序为三点按逆时针排列，

S=1/2[(x1y2-x2y1)+(x2y3-x3y2)+(x3y1-x1y3)]。

找点D（-3,-1）,E（4,-1）,F（4,6）..连接A、D,连接D、E,连接E、F 连接A、F

用矩形面积ADEF=7*7=49减去三角形ABD面积=7*2/2=7、三角形BCE=5*3/2=7.5、ACF=4*7/2=14的面积,最后等于20.5

扩展资料：

行列式的概念是从解线性方程组的需要中引进来的。所谓线性方程组是指未知项的最高次数是一次的方程组，其中最简单的是在中学时学习的二元线性方程组：

其中

xj表未知量，aij称系数，bi称常数项。

称为系数矩阵和增广矩阵。若x1=c1，x2=c2，…，xn=cn代入所给方程各式均成立，则称（c1，c2，…，cn）为一个解。若c1，c2，…，cn不全为0，则称（c1，c2，…，cn）为非零解。若常数项均为0，则称为齐次线性方程组，它总有零解（0，0，…，0）。两个方程组，若它们的未知量个数相同且解集相等，则称为同解方程组。线性方程组主要讨论的问题是：

①一个方程组何时有解。

②有解方程组解的个数。

③对有解方程组求解，并决定解的结构。这几个问题均得到完满解决：所给方程组有解，则秩(A）=秩（增广矩阵）；若秩(A）=秩=r，则r=n时，有唯一解；r<n时，有无穷多解；可用消元法求解。

当非齐次线性方程组有解时，解唯一的充要条件是对应的齐次线性方程组只有零解；解无穷多的充要条件是对应齐次线性方程组有非零解。但反之当非齐次线性方程组的导出组仅有零解和有非零解时，不一定原方程组有唯一解或无穷解，事实上，此时方程组不一定有 ，即不一定有解。

克莱姆法则（见行列式）给出了一类特殊线性方程组解的公式。n个未知量的任一齐次方程组的解集均构成n维空间的一个子空间。