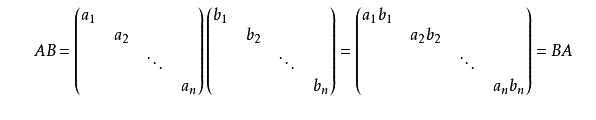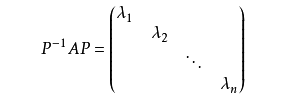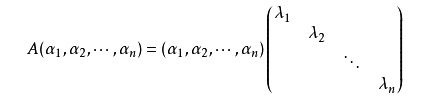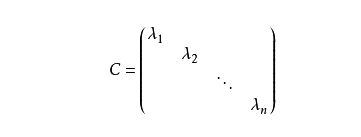知道一个矩阵如何求一个矩阵的一百次方

当知道一个矩阵时，可以利用矩阵相似对角化的方法来求一个矩阵的一百次方。

如果存在一个矩阵P，使 P逆*A*P的结果为对角矩阵，则称矩阵P将矩阵A对角化。其中P为可以矩阵，即可得P逆*A*P=C，其中C为对角矩阵。

又因为同阶对角矩阵的乘积仍为对角阵，且它们的乘积是可交换的，即

所以可以知道对角矩阵的一百次方就等于对角矩阵的主对角元素上的数值的一百次方。

同时根据可逆矩阵的性质，可以知道 P逆*P=E，其中E为单位矩阵。

可以这样推导

因为 P逆*A*P=C，所以（P逆*A*P）^100=c^100；

所以P逆*A*(P*P逆)*A*(P*P逆)……(P*P逆)*A*P=c^100；

最后约得P逆*A^100*P=c^100；再一次矩阵等式可逆转化得A^100=P*c^100*P逆。

由此可以求出 A^100=P*c^100*P逆。

扩展资料：

矩阵相似于对角矩阵的充要条件：

n阶矩阵A相似于对角矩阵的充要条件是A有n个线性无关的特征向量。

1、必要性。

设有可逆矩阵P，使得

令矩阵P的n个列向量为α1，α2，……αn，则有

2、充分性

由必要性的证明可见，如果矩阵A有n个线性无关的特征向量，设它们为α1，α2，……αn，对应的特征值分别为λ1，λ2，……λn，则有Aαi=λiαi（i=1,2，……，n），以这些向量为列构造矩阵P，则P可逆，且AP=PC，其中C为对角矩阵

参考资料来源：百度百科-对角化

参考资料来源：百度百科-对角矩阵

参考资料来源：百度百科-可逆矩阵