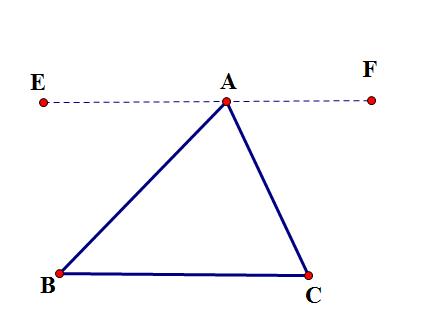
已知：三角形abc，求证：角a+角b+角c=180°证明方法有多种

证明：

过点A作EF//BC。

∵EF//BC，

∴∠EAB=∠B，∠FA潮贾篡绐C=∠C（两直线平行，内错角相等），

∵∠BAC+∠EAB+∠FAC=180°（平角180°），

∴∠BAC+∠B+∠C=180°（等量代换），

即∠A+∠B+∠C=180°。

三角形性质：

1 、在平面上三角形的内角和等于180°（内角和定理）。

2 、在平面上三角形的外角和等于360° (外角和定理)。

3、 在平面上三角形的外角等于与其不相邻的两个内角之和。

推论：三角形的一个外角大于任何一个和它不相邻的内角。

4、 一个三角形的三个内角中最少有两个锐角。

5、 在三角形中至少有一个角大于等于60度，也至少有一个角小于等于60度。

6 、三角形任意两边之和大于第三边，任意两边之差小于第三边。

7、 在一个直角三角形中，若一个角等于30度，则30度角所对的直角边是斜边的一半。

8、直角三角形的两条直角边的平方和等于斜边的平方（勾股定理）。

*勾股定理逆定理：如果三角形的三边长a，b，c满足a²+b²=c² ，那么这个三角形是直角三角形。

9、直角三角形斜边的中线等于斜边的一半。

10、三角形的三条角平分线交于一点，三条高线的所在直线交于一点，三条中线交于一点。

11、三角形三条中线的长度的平方和等于它的三边的长度平方和的3/4。

12、 等底同高的三角形面积相等。

13、 底相等的三角形的面积之比等于其高之比，高相等的三角形的面积之比等于其底之比。

14、三角形的任意一条中线将这个三角形分为两个面积相等的三角形。

15、等腰三角形顶角的角平分线和底边上的高、底边上的中线在一条直线上（三线合一）。

16、 在同一个三角形内，大边对大角，大角对大边。