Mathematica 泊松分布

1、Mathematica中，泊松分布的符号是PoissonDi衡痕贤伎stribution[参数]使用PDF求出其概率函数如图，即泊松分布定义式。CDF则求出泊松分布的累积分布。

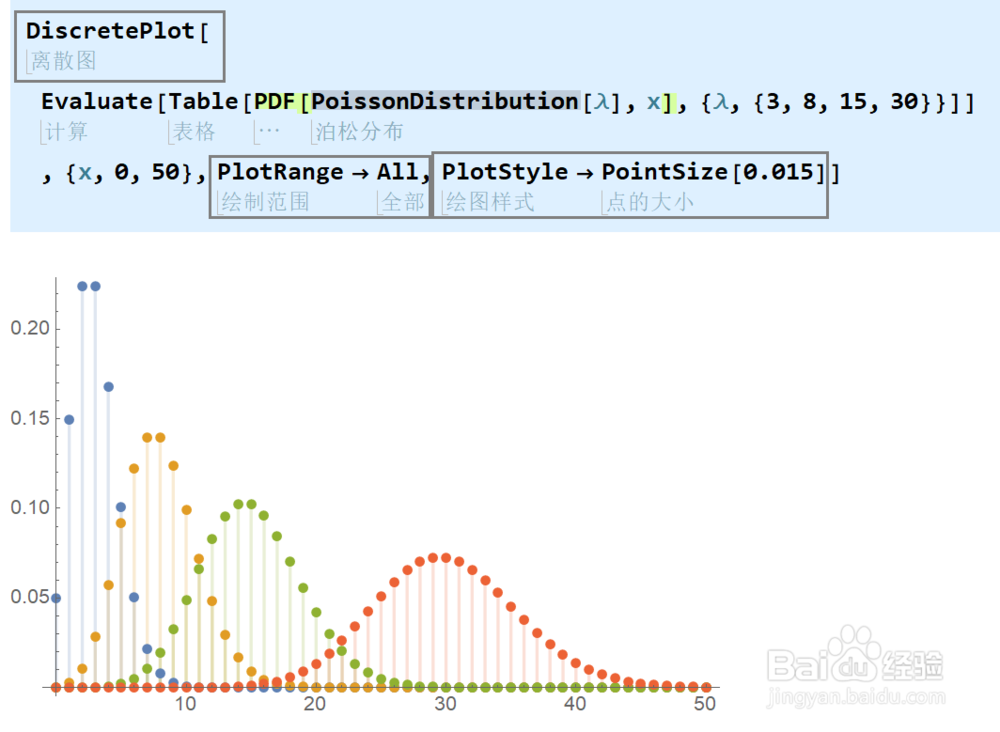
2、使用DiscretePlot可以绘制离散函数。如图代码分别绘制泊松分布参数为3,8,15,30时的图线形状。随着参数增大，泊松分布均值逐渐增大且变得对称。

3、使用Mean求得泊松分布平均值为μ，方差正好也是μ。下面我们分别推导这两个结论。

4、在Mathematica中，我们观察公式，逐步化简。并使用FullSimplify随时验证化简是否正确。最终求得平均值μ。

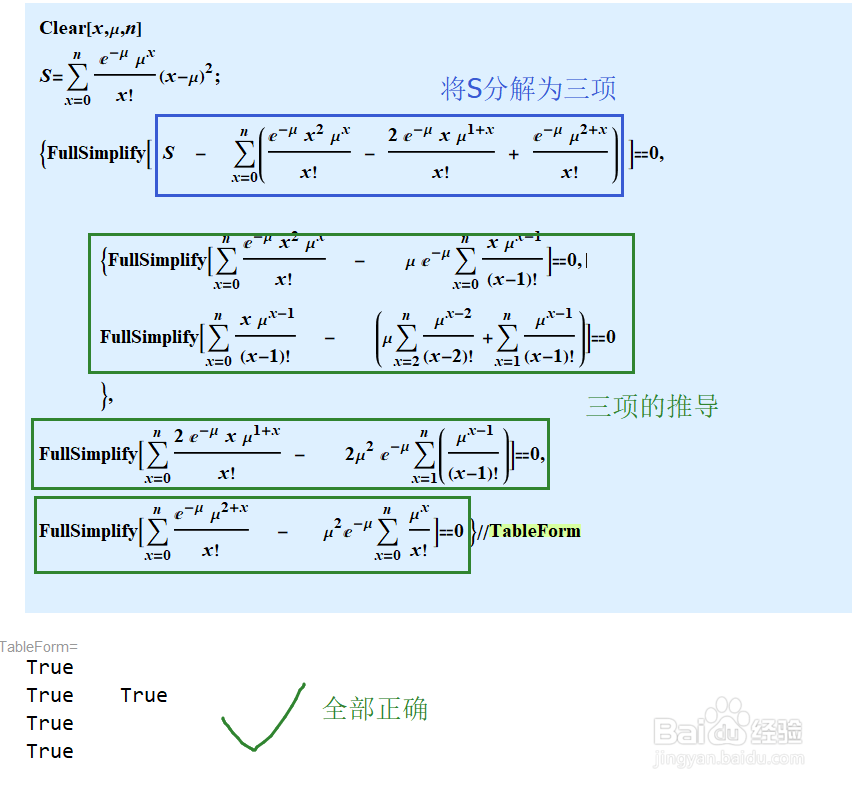
5、方差的推导稍稍麻烦一些。首先把方差式子展开成三项，分别化简每一项。其中第一项展开成两个可以求的求和。化解年过程如图。

6、使用无穷求和分别验证a,b,c三项，和我们自己化简取极限得到的结果一致。最终a-b+c得到方差的计算结果为μ。

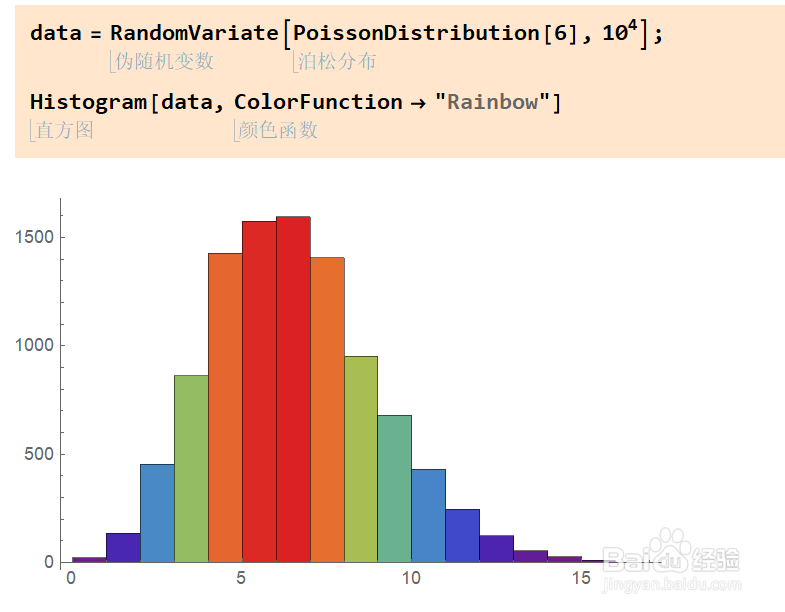
7、使用RandomVariate函数，第一个参数为泊松分布以生成符合泊松分布的伪随机数。使用Histogram绘制其直方图图案。