多目标优化的解决方法

1、任何多目标规划问题，都由两个基本部分组成：两个以上的目标函数；若干个约束条件。

2、对于多目标规划问题，可以将其数学模型一般地描写为如下形式：

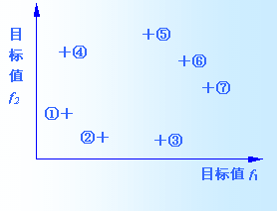
3、在图中，max(f1, f2) .就方案①和②来说，①的 f2 目标值比②大，但其目标值 f1 比②小，因此无法确定这两个方案的优与劣。

4、在各个方案之间，显然：④比①好，⑤比④好, ⑥比②好, ⑦比③好。

5、而对于方案⑤、⑥、⑦之间则无法确定优劣，而且又没有比它们更好的其他方案，所以它们就被称为多楫默礤鲼目标规划问题的非劣解或有效解，其余方案都称为劣解。所有非劣解构成的集合称为非劣解集。

6、当目标函数处于冲突状态时，就不会存在使所有目标函数同时达到最大或最小值的最优解，于是我们只能寻求非劣解（又称非支配解或帕累托解）。

7、为了求得多目标规划问题的非劣解，常常需要将多目标规划问题转化为单目标规划问题去处理。实现这种转化，有如下几种建模方法。

8、效用最优化模型思想：规划问题的各个目标函数可以通过一定的方式进行求和运算。这种方法将一系列的目标函数与效用函数建立相关关系，各目标之间通过效用函数协调，使多目标规划问题转化为传统的单目标规划问题：在用效用函数作为规划目标时，需要确定一组权值 li 来反映原问题中各目标函数在总体目标中的权重。

9、罚款模型思想: 规划决策者对每一个目标函数都能提出所期望的值（或称满意值）；在加权的基础上通过比较实际值 fi 与期望值 fi* 之间的偏差来选择问题的解

10、约束模型理论依据 ：若规划问题的某一目标可以给出一个可供选择的范围，则该目标就可以作为约束条件而被排除出目标组，进入约束条件组中。

11、假如，除第一个目标外，其余目标都可以提出一个可供选择的范围，则该多目标规划问题就可以转化为单目标规划问题：目标达到法目标规划模型了解概念，其他用到了再说。