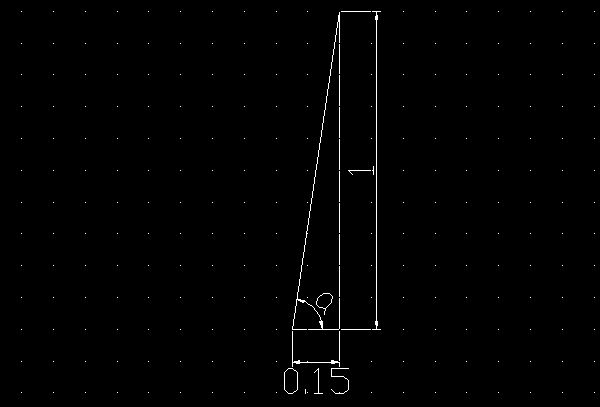
已知坡比为1:0.15高为0.8m，斜长为多少，需要简单点的计算式

已知坡比为1:0.1猱蝰逾鸾5高为0.8m，斜长为0.80895。

计算方法如下：

t锾攒揉敫ana=1/0.15=100/15=20/3

sina=20/√409

cosa=3/√409

高：斜长=sina=20/√409

斜长=0.8÷20/√409=0.80895。

扩展资料：

坡面的垂直高度h和水平宽度l的比，即坡角的正切值 (tan∠a值∠a为斜坡与水平面夹角)。「亦即tan∠α」。通常用“i”表示。

角a的正切=垂直距离/水平距离，也可写作：tan∠α=h/l。

坡面的垂直高度(h)和水平宽度(l)的比叫做坡度（或坡比）。

设坡角为α，坡度为k，则k=h:l=tanα；

坡度一般写成1∶m的形式，其中m=1/k，m称为边坡系数,

坡度越大，则坡角越大，坡面就越陡，如1：2>1：3，则1：2对应的坡角大，坡面较陡。

1：m可理解为：高=1，宽=m；即坡度=tanα=h：l=1：m 。

坡面的垂直高度(h)和水平宽度(l)的比叫做坡度（或坡比）。

设坡角为α，坡度为i，则

坡度一般写成1∶m的形式。

坡度越大，则坡角越大，坡面就越陡。

坡度与坡角的关系是i=tan a。

在学习锐角三角函数时，出现过坡度这个名词。

在修堤、筑坝、开渠、挖河时，我们常常需要表示斜坡的倾斜程度。在上坡公路旁的指示牌上也常看到坡度的标志。图中，坡面的铅直高度h和水平宽度l的比叫做这个斜坡的坡度 。若用i表示坡度，则有i=h/l由坡度的意义可知，“坡度”是一个比值，它并不是表示一个角度。

我们把斜坡面与水平面的夹角叫做坡角 ，若用α表示，可知坡度与坡角的关系是i=h/l=tanα

由于在0°<α<90°内，tanα是增函数，即当坡角α增大时，坡度也随之变大。由此可见，斜坡坡角越大，则坡度也越大，也就是说坡面就越陡。

由此可见，坡角表示一个角，坡度表示这个角的正切函数，二者的区别是明显的。

我们日常生活中常把一个斜坡的角度理解为坡度。例如，汽车上坡困难，我们就说：“这个山坡坡度太大。”实际上说这句话的意思是表示“这个山坡的坡角太大”，但生活中并不这样讲。因此就容易把这种误解带进数学学习中，把坡度与坡角两个不同的概念混淆了。

参考资料来源：百度百科-坡比

参考资料来源：百度百科-坡角