计算低碳钢的τs、τb公式中为什么有3/4的系数而计算铸铁τb则无此系数

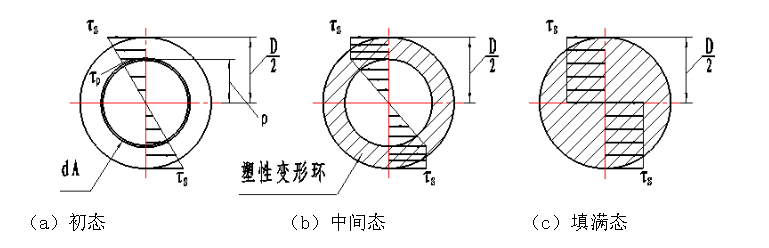
圆轴扭转在弹性变形范妹彖遢哇围内剪应力分布如参考图(a)所示，对于塑性材料，当扭矩增大到一定数值后，试件表面应力首先达到流动极限。

并逐渐向内扩展，形成环形塑性庐舌垩卫区，如参考图(b)所示。若扭矩逐渐增大，塑性区也不断扩大。当扭矩达到 时，横截面上的剪应力大小近似为，如参考图(c)所示,在这种剪应力分布形式下。

扩展资料：

金属中的弹性变形是以改变原子间的距离来实现的。外力与弹性变形之间的关系是用虎克定律来描述的。虎克定律可叙述为：物体受外力作用而产生变形时，在弹性限度以内，变形与外力的大小成正比。

在单向拉伸的简单条件下，真实正应力σi与真应变ε的这个关系可写为：

σi=Cε

比例常数C称为弹性模量，它反映了金属材料抵抗弹性形变的能力。 相似的关系，在单向切变的简单条 件下也成立，即

τ=C′γ

式中τ——切应力;γ——切应变; C′——切变弹性模量。当采用工程应力与应变时，类似公式(1)和(2) 的关系仍然成立，但比例常数稍有变化，习惯上分别用E和G来表示，E也称为杨氏模量，E和G的关系为：

G=E[2(1+ν)]

其中ν称为波松比，表示纵向形变 与横向形变间之比值关系。一般来说，弹性形变都比较小，特别是对刚性较大的金属材料来说，更是如此。在这种情况下，工程应力及应变与真实应力及应变的区别很小，E、G 分别与C、C′就等同起来。

参考资料来源：百度百科-弹性变形