数学中最短距离的解题思路

在初中数学的学习中，可能会遇到很多不同的习题，然而考试的解题方法如出一辙，都不会有太大的变动。比如最短距离的解题

审题

1、首先做数学习题，我们必须学会审题。这次我们主要学讲的是 最短距离。那么我们就要知道什么是最短距离：两点之间先端最短。

2、其次，学会变通，把最短距离的问题转会到线段的考点。

3、最后。计算。初中生最大的毛病就是太依赖计算器，在高考中是不允许的。

典型习题分析解答

1、在直线AB的两侧有两个不同的点C,D，求直线上一点p，使得PD+PC最小？两点之间线段最短，直接链接CD,与直线AB的交点就是所求的点P

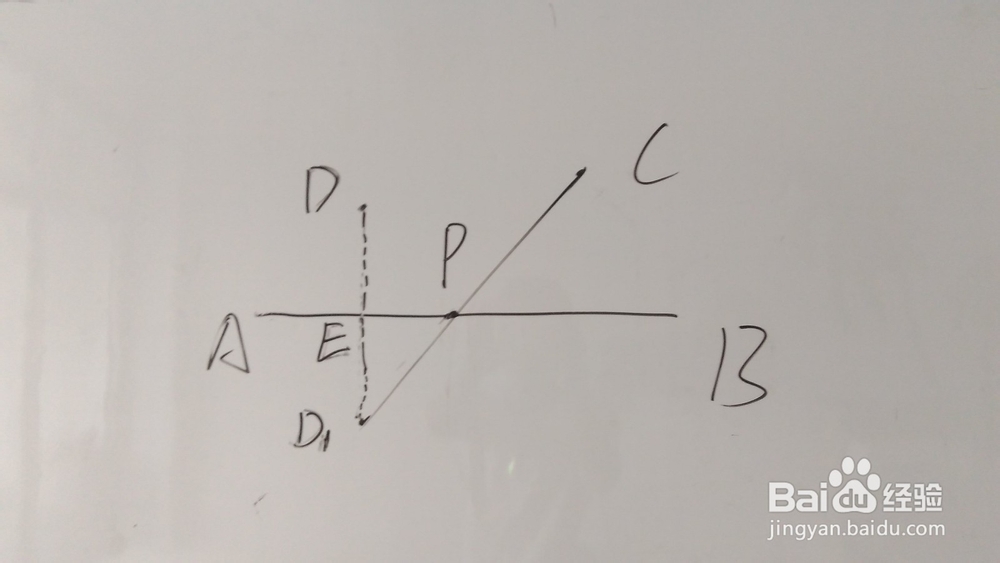
2、在直线AB的一侧有两个不同的点C,D，求直线上一点p，使得PD+PC最小？先转换到锂淅铄旰直线两侧有两个不同的点，所以先做DE垂直AB,并延长DE=D1E,链接CD1，与直线的交点就是P点的位置。

3、在正方形ABCD中，AB=4,DE=1,链接对角线AC,在AC上有一点P,使得PE+PD最小？先做D关于直线AC的垂线，并延长。此时D1点与B点重合，链接BE与AC的交点就是所求的P点

4、在菱形ABCD中，AB=2,E为AB边的中点，P为对角线AC上一动点，求PE+PB最小值?做B垂直与AC，并延长，发现B1与D重合，所以链接ED，ED与AC的交点就是P点。