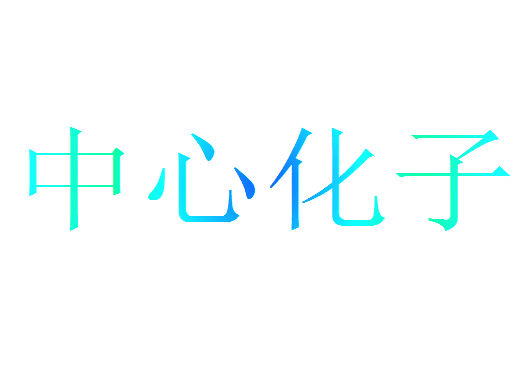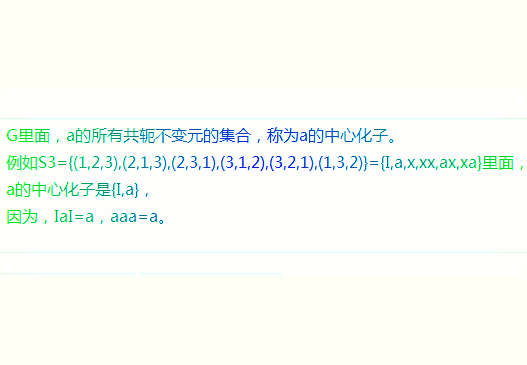怎么理解群论里面的共轭的相关概念

群论里面，一个重要的概念，就是共轭。那么，应该怎么系统的学习共轭呢？本文，就通过具体的例子，来介绍一下与共轭有关系的概念。

工具/原料

电脑

Mathematica

共轭的定义

1、设a和x是群G里面的元素，y是垓矗梅吒x的逆元素，那么，xay称为a关于x的共轭。比如，在3阶置换群S3里面：单位元是I=(1,2,3)——也就是不置换；锾攒揉敫a=(2,1,3)——对换前两个元素；x=(2,3,1)——轮换，把第一个元素放到最后面。那么，x的逆元素，就是y=xx=(3,1,2)；a关于x的共轭，就是xay=xa(3,1,2)=x(1,3,2)=(3,2,1)。而ax也是(3,2,1)，所以，a关于x的共轭 xay=ax。

2、a关于G里面每一个元素，都有一个共轭，这些共轭的集合，称为a的共轭类。比如，在S3里面，a=(2,1,3)的共轭类是可以逐个求出来的：S3={(1,2,3),(2,1,3),(2,3,1),烫喇霰嘴(3,1,2),(3,2,1),(1,3,2)}={I,a,x,xx,ax,xa}，其中，a的逆元素是a，x的逆元素是xx，ax的逆元素是ax，xa的逆元素是xa，那么，a关于I的共轭是a；a关于x的共轭是xaxx=ax；a关于xx的共轭是xxax=xa；a关于ax的共轭是axaax=axx=xa；a关于xa的共轭是xaaxa=xxa=ax；所以，a在S3里面的共轭类是{a,ax,xa}。

中心化子

1、共轭不变：给定G的元素a，如果对某个G中的元素x，a关于x的共轭等于a，那么，就说x是a的共轭不变元。例如S3={(1,2,3),(2,1,3),(2,3,1),(3,1,2),(3,2,1),(1,3,2)}={I,a,x,xx,ax,xa}里面，a关于I的共轭等于a，那么I就是a的共轭不变元。

2、G里面，a的所有共轭不变元的集合，称为a的中心化子。例如S3={(1,2,3),(2,1,3),(2,3,1),(3,1,2),(3,2,1),(1,3,2)}={I,a,x,xx,ax,xa}里面，a的中心化子是{I,a}，因为，IaI=a，aaa=a。

3、中心化子与共轭类有一个重要联系，那就是：如果G里面有n个元素，a的共轭类有m个元素，那么，a的中心化子就有荏鱿胫协n/m个元素。这里需要注意，m能整除n，这一点很重要。比如，在S3={(1,2,3),(2,1,3),(2,3,1),(3,1,2),(3,2,1),(1,3,2)}={I,a,x,xx,ax,xa}里面，S3有6个元素，a的共轭类有3个元素，a的中心化子有2个元素，进而有，6=2*3。

群的中心

1、设o是G里面的元素，且o的中心化子是整个群G，那么，所有这样的o的集合，称为G的中心。实际上，群的中心，就是群里面所有元素的中心化子的交集。比如，S3={(1,2,3),(2,1,3),(2,3,1),(3,1,2),(3,2,1),(1,3,2)}={I,a,x,xx,ax,xa}，那么，S3的中心，就只能是{I}。

2、G的元素a属于G的中心，当且仅当a的中心化子是整个群G。比如在S3里面：I的中心化子是这个S3，I的共轭类是{I}，6=6*1。

正规子群

1、设N是G的子群，如果N里面的任意元素关于G的共轭仍旧属于N，就说N是G的正规子群。S3的正规子群有两个——{I}和S3。