画指数复合函数y=0.5^(-6x^2+5x+4)的图像

1、函数的定义域，根据函数特征，函数自变量可以取全体实数，即定义域为：(-∞，+∞）。

2、函数的单调性，通过函数的一阶导数，求出函数的驻点，再根据驻点判断导数的符号，即可得函数的单调区间。

3、如果函数y=f(x)在区间D内可导(可微)，若x∈D时恒有f'(x)>0，则函数y=f(x)在区间D内单调增加;反之亦然。

4、函数的凸凹性，通过函数的二阶导数，得函数的拐点，解析函数的凸凹区间。

5、函数的极限，函数在无穷远处的极限计算如下：

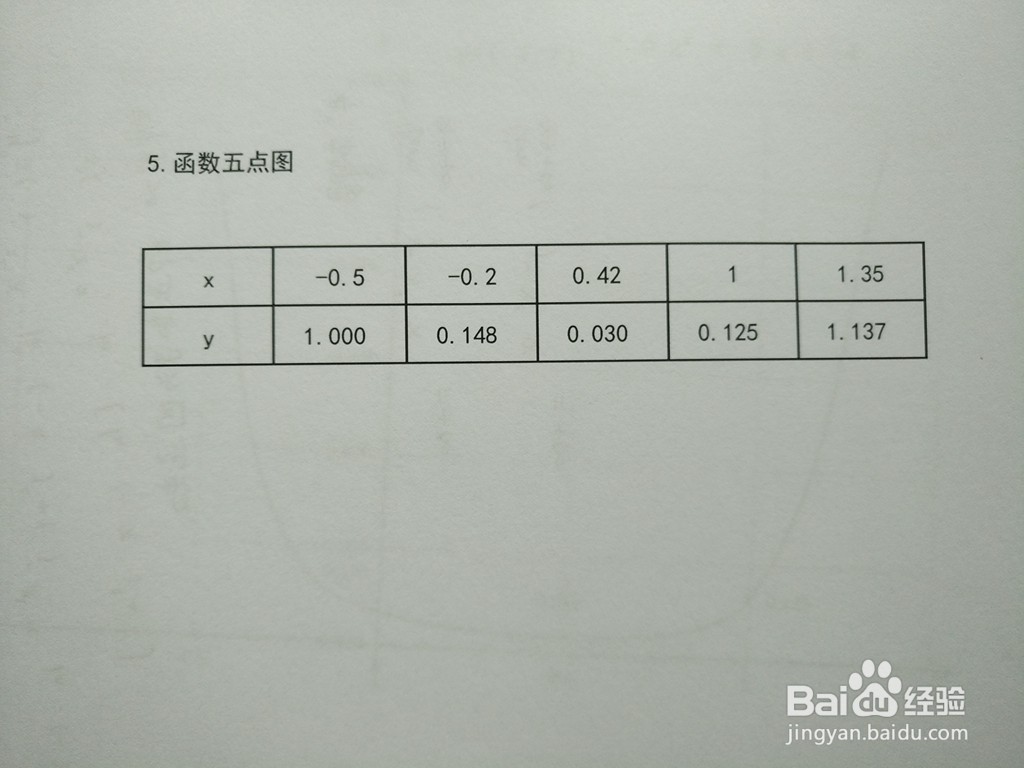
6、用列表法，列出函数上部分点解析表：

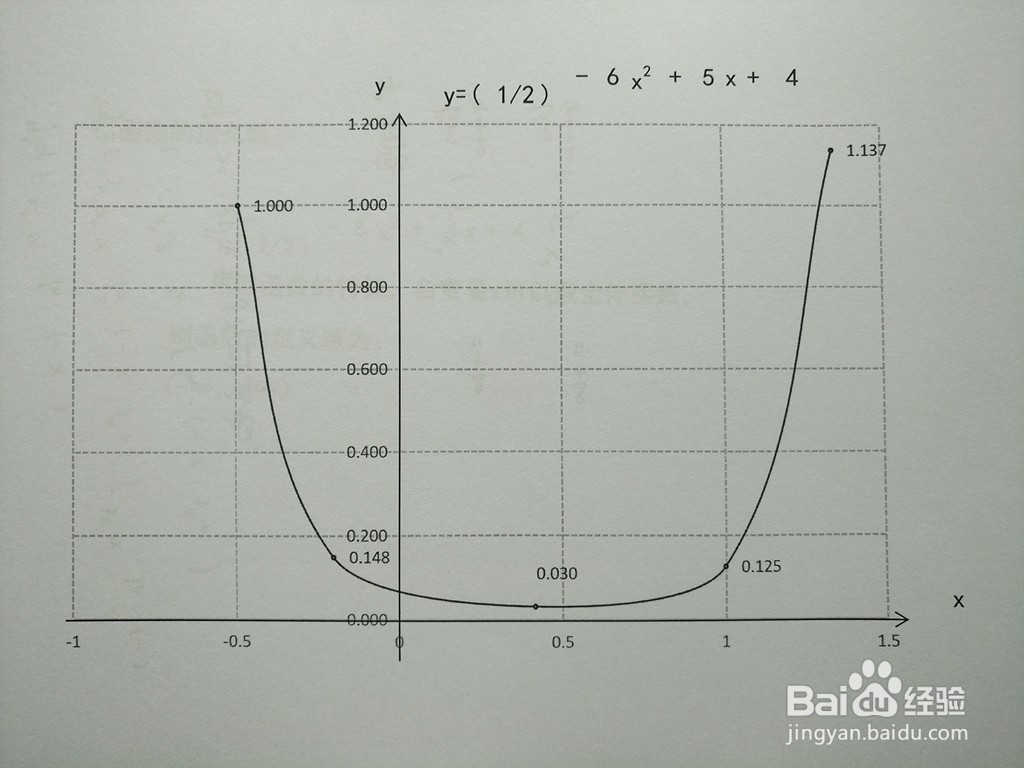
7、综合以上函数的定义域、单调、凸凹、极限等性质，函数的示意图如下：