思维训练 举一反三

在孩童教育中，思维训练永远是重要的话题。如果把思维训练融入到家庭的玩耍之中，那将是最开心的事了，不但事半功倍，也增加了多多的亲情。 思维训练的办法很多。以下是最小成本，却最有效果的方法。为喜欢的家长，举一反三之用。

一、思维训练题目

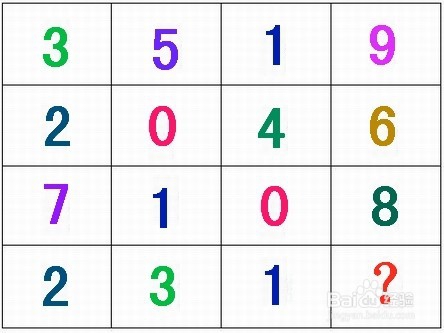
1、方格填数 如图，是四排、四列的表格，上面写满了数字。根据数字间的规律，请在右下角的“？”处，填入合适的数字。

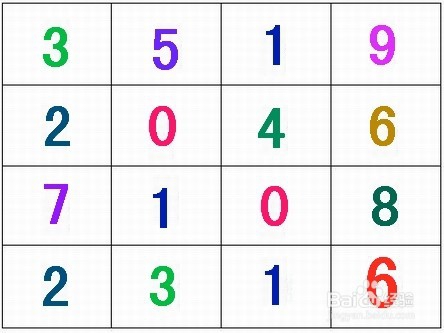
2、方格填数“6”： 找到规律了吗？很简单，把前三列的数相加，等于第四列的数： 第一行：3＋5＋1=9 第二行：2＋0＋4=6 第三行：7＋1＋0=8 所以：第四行：2＋3＋1=6 结果：在“？”处填写6。

二、补全算式

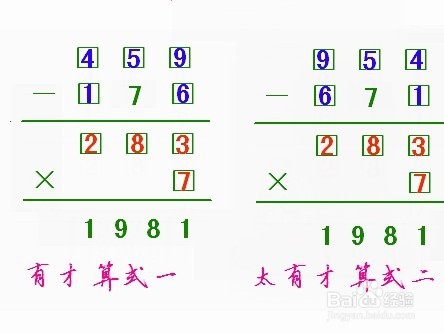
1、残缺的算式 如图，是个残缺的算式，你需要好好动动脑筋，把1、2、3、4、5、6、7、8、9这九个数分别填入“□”小方框中，使算式成立？

2、起步艰难 我们只知道得数是“1981”，所以先要从乘法部分推导。 看“1981”的尾数是1，乘法中只有9×9和3×7的尾数能得到“1”，9×9要用两个9，和题意不符，故取3×7。如图，3放下面为乘数，7为被乘数的尾数。进一步，三、七得二十一后，写1，进2，要和“1981”的“8”对上，还需要个“6”，所以被乘数中间的数字只能是2，二、三得六，加二得八，推导顺利。 可是，再往下就不行了，什么数乘以3能得19呀？推演到此止步，如图。

3、重捋思路 开始的思路是对的，是不是“3”和“7”的位置搞错了。如图，调整为7为乘数，3为被乘数的尾数。 同样是三、七得二十一，写1，进2，“7”和什么数相乘尾数是“6”？只有8。所以被乘数中间的数字填写8，被乘数前面的数字填写2（只能填2）。仔细看一遍，乘法部分推导成功了！如图。

4、缜密思维 相对而言，减法部分就容易一些。现在我们知道，还有剩下的1、4、5、6、9五个墙绅褡孛数，还知棕百脾酷道减法部分的得数“差”是“283”。要使这个“差”的个位是3的，只能有9－6和4－1两种可能，我们分别试一试： ①在“被减数”的个位填写9，“减数”的个位填写6。再推导“被减数”的中间数字。什么数减7等于8？当然是15，这就确定了“被减数”中间数字是5，剩下的4和1就好办了，4填写在上面，1填写在下面，检查一遍，成功了，如图。 ②换一换，看看能否可行。 “被减数”的个位填写4，“减数”的个位填写1。“被减数”中间数字还是填5，剩下的9和6分别填写在上面和下面，检查一遍，也成功了，如图。

三、推理判断

1、瓶子里装的是什么？ 有四个不透明的瓶子，分别装有四种饮品：白酒、啤酒、可乐、果汁。四个瓶子上都贴有标签，已知只有果汁瓶子上贴的标签是错的，或说是假的，即指向错误。而其他瓶子上的标签，标识指向都正确。根据以下标签上的内容（如图），你能推断出每个瓶子里装的是什么饮品吗？ ①甲瓶标签：乙瓶装的是白酒 ②乙瓶标签：丙瓶装的不是白酒 ③丙瓶标签：丁瓶装的全是可乐 ④丁瓶标签：此标签是最后贴上去的

2、推断瓶子中的物质 从4条信息看，第④信息是没用的。我们还是用排除法逐个分析。 首先，假设甲瓶里装的是果汁，则甲瓶标签内容错误，即由①推出乙瓶装的就不是白酒；其他瓶子的标签就都是正确的了，从②推断出“丙瓶装的不是白酒”；从③推断出“丁瓶装的是可乐”；这样，甲瓶是果汁，丁瓶是可乐，乙瓶和丙瓶都不是白酒，那么，白酒装到哪里去了？显然，假设是不成立的。 再设，假设乙瓶里装的是果汁，则乙瓶标签内容错误，即由②推出丙瓶里装的就是白酒；可是，甲瓶里没装果汁，其标签应该是正确的，由①可知，乙瓶装的是白酒，两个瓶子都装白酒，显然推出了矛盾。所以原设不成立，即乙瓶没装果汁。 往下，假设丙瓶里装的是果汁，则丙瓶标签内容错误，即由③推出丁瓶里装可乐为假；其他标签都正确，则由①，乙瓶装的是白酒；丁瓶不装可乐，就只能装啤酒；可乐装到了甲瓶里。这样，原设成立，即得结论：甲瓶装可乐，乙瓶装白酒，丙瓶装果汁，丁瓶装啤酒。如图。 顺便，你也可假设丁瓶装果汁，这和③矛盾，即假设不能成立。