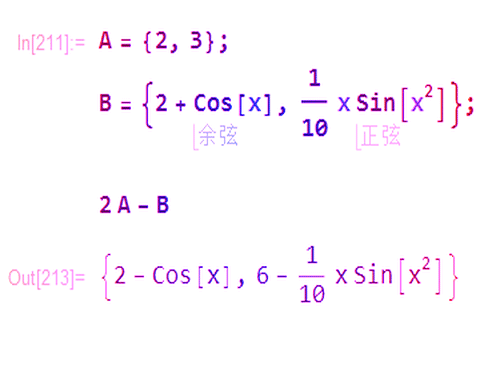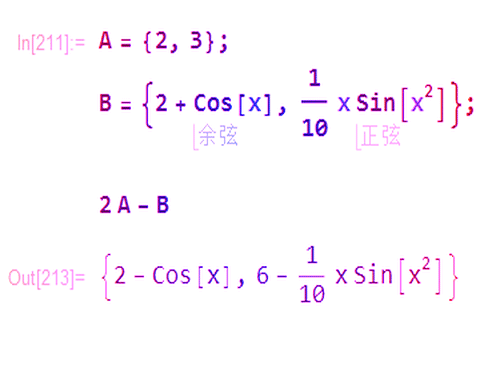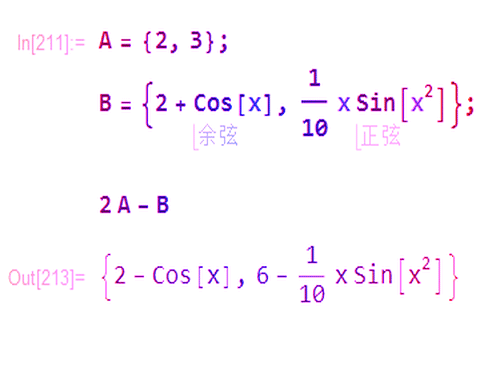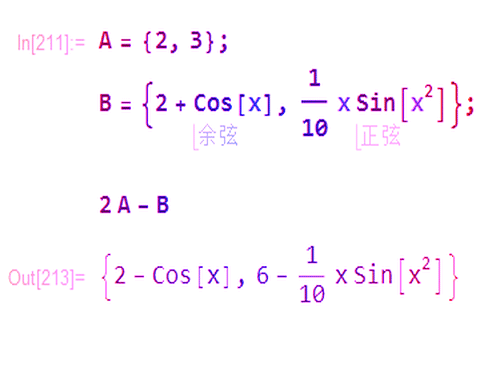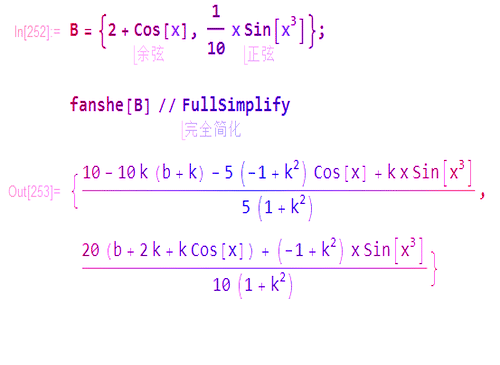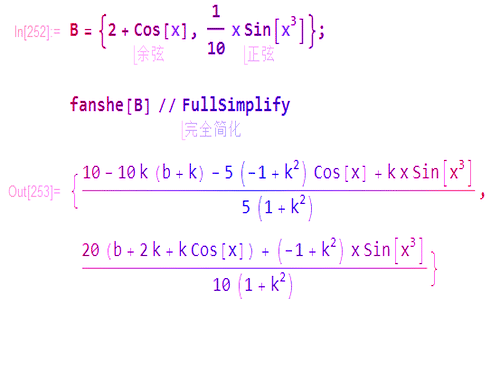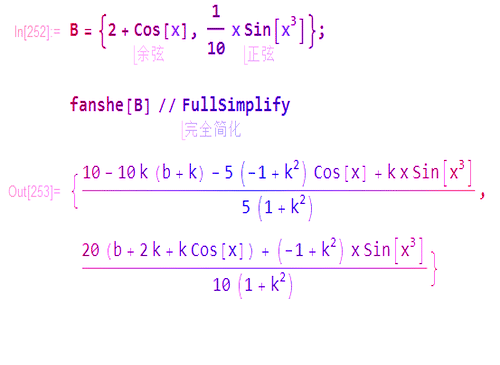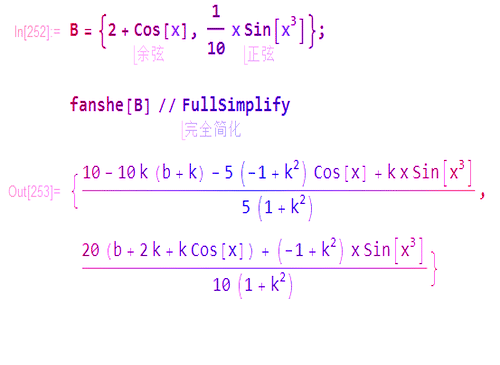怎么用计算机描述对称变换

初等几何变换，除了平移和旋转，还应该包括对称变换，包括点对称、轴对称和面对称。那么，如果我们酋篚靶高需要用计算机处理这类问题的时候，必须把唁昼囫缍这些变换，变成计算机语言，然后才能用于计算。Mathematica很好地解答了这类问题。

工具/原料

电脑

Mathematica

中心对称

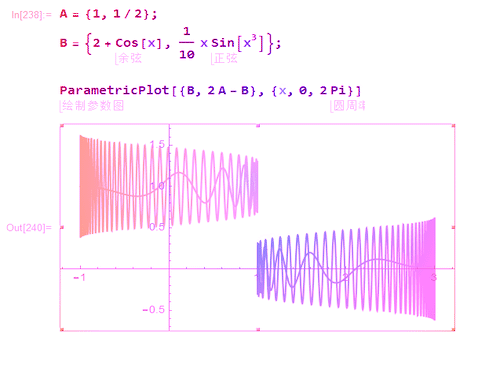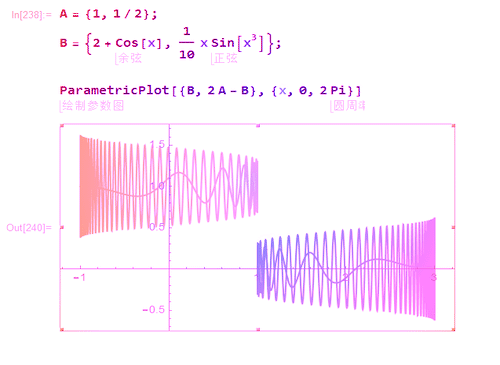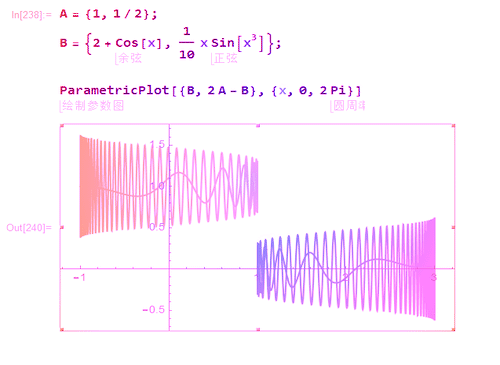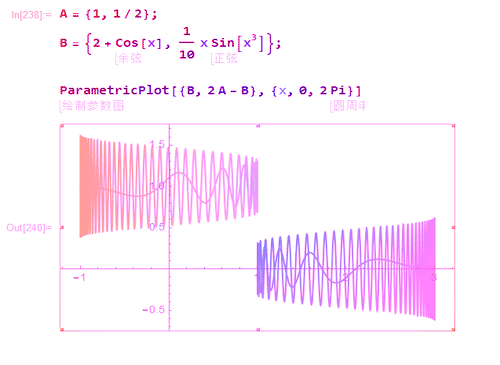
1、给定点A和B，那么B关于A的对称点，就是2A-B。

2、图形也能够体现出这一点。

轴对称

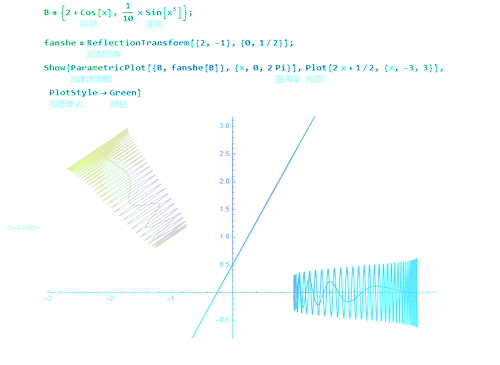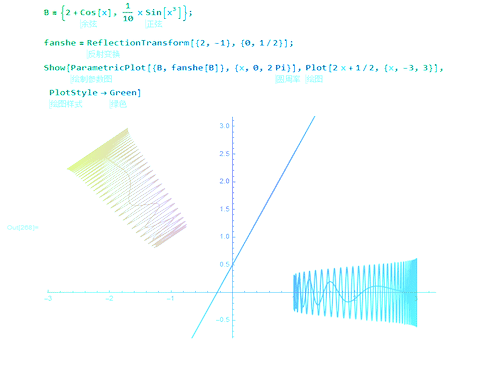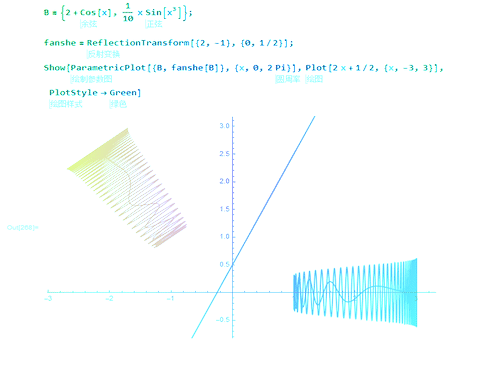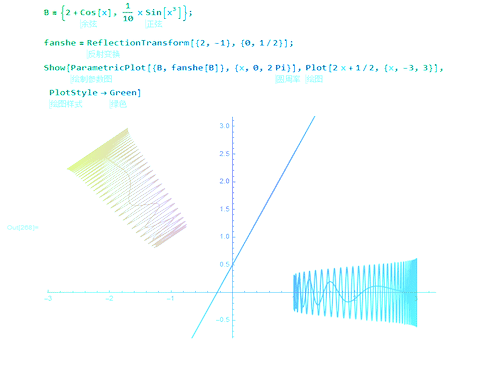
1、直线y=kx+b经过点(0,b)，其法向量是：(k,-1)，那么关于这条直线的对称变换可以描述为：ReflectionTransform[{k, -1}, {0, b}]

2、用它直接作用于几何图形：fanshe[B] // FullSimplify

3、给k和b赋以具体的数值，就可以绘图：fanshe = ReflectionTransform[{2, -1}, {0, 1/2}]两个图形关于直线y=2x+0.5对称。

面对称

1、平面ax+by+cz=0过(0,0,0)点，它的法向量是(a,b,c)，痘痉颔湄那么，关于这个平面的对称变换，就是：jingmian=ReflectionTransform[{a,b,c}]

2、平面方程是：a(x-1)+b(y-2)+c(z+1)=0，关于这个平面的对称变换：ReflectionTransform[{a, b, c}, {1, 2, -1}]

3、要画图，就需要把a、b、c具体化：2 (x - 1) + 3 (y - 2) - 1 (z + 1) == 0