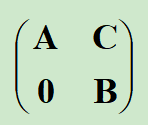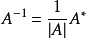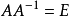上三角或下三角矩阵的逆矩阵能否简便方法求出只有主副对角线不为0的矩阵能否直接写出逆矩阵。

1、上三角矩阵的逆矩扃渚释夭阵

将上三角矩阵划分成块矩阵，如上图所示，则其逆矩阵结果如下图。

2、下三角矩阵的逆矩阵

将下三角矩阵划分成块矩阵，如上图所示，则其逆矩阵结果如下图。

3、只有主对角线不为零的矩阵

主对角元素取倒数，原位置不变。

4、只有副对角线不为零的矩阵

副对角元素取倒数，位置颠倒。

示例如下：

扩展资料

矩阵求逆的求法

（1）初等变换法，通过初等变换将A矩阵变换成单位矩阵，则对应的单位矩阵变换成B矩阵，B矩阵即为A矩阵的逆矩阵，（A I）->（I B）；

（2）伴随阵法，公式为：

（3）利用定义求逆矩阵

设A、B都是n阶方阵，如果存在n阶方阵B使得AB=BA=E，则称A为可逆矩阵，而称B为A的逆矩阵。

（4）恒等变形法

恒等变形法求逆矩阵的理论依据为逆矩阵的定义，此方法也常用与矩阵的理论推导上，就是通过恒等变形把要求的值化简出来，题目中的逆矩阵可以不求，利用

参考资料来源：百度百科--矩阵求逆