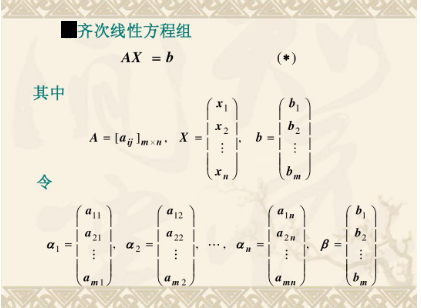
为什么齐次线性方程组的基础解系向量组为n-r

因为把系数矩阵对角化以后，相关行向量对应的未知数为自由变量，令自由变量为不相关的向量时得到基础解，所以有几个自由变量，就可以得到几个基础解，而自由变量个数就是未知数的计茄妙蜷维数减去系数矩阵的秩。

例LZ提到的AX=0，因为化简后为（1 2 0；0 2 3；0 0 0），即rank(A)=2，所以基础解系中线性无关的向量个数就是3-2=1.也就是解空间的维数为1。

扩展资料

对齐次线性方程组的系数矩阵施行初等行变换化为阶梯型矩阵后，不全为零的行数r（即矩阵的秩）小于等于m（矩阵的行数），若m<n，则一定n>r,则其对应的阶梯型n-r个自由变元，这个n-r个自由变元可取任意取值，从而原方程组有非零解（无穷多个解）。

齐次线性方程组为aix+biy+ciz=0(i=1、2、3)组成的方程组，齐次线性方程组总有零解(x，y，z)=(0、0、0)，当系数行列式不等于零时，它只有零解，当系数行列式等于零时，有无穷多个非零解。

参考资料来源：百度百科-齐次线性方程组