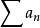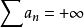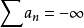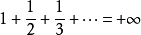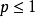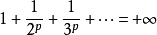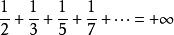2个无穷大与无穷大的乘积是无穷大吗

无穷大与无穷大的乘积是无穷大。

若自变量x无限接近x0（或|x|无限增大）时，函数值|f(x)|无限增大，则称f(x)为x→x0(或x→∞)时的无穷大量。例如f(x)=1/(旌忭檀挢x-1)^2是当x→1时的无穷大量，f(n)=n^2是当n→∞时的无穷大量。无穷大量的倒数是无穷小量。应该特别注意的是，无论多么大的常数都不是无穷大量。

性质：

1.两个无穷大量之和不一定是无穷大；

2.有界量与无穷大量的乘积不一定是无穷大（如常数0就算是有界函数）；

3.有限个无穷大量之积一定是无穷大。

4.一个数列不是无穷大量，不代表它就是有界的（如，数列1，1/2，3，1/3，……）。

扩展资料：

对于发散至正无穷大（或负无穷大）的无穷级数

例：

调和级数：

更一般地，对于p级数，

时有

素数的倒数之和：

如，可数集合，如自然数集，整数集乃至有理数集对应的基数被定义为“阿列夫零”。比可数集合“大”的称之为不可数集合，如实数集，其基数与自然数的幂集相同，为二的阿列夫零次方，被定义为“阿列夫壹”。

由于一个无穷集合的幂集总是具有比它本身更高的基数，所以通过构造一系列的幂集，可以证明无穷的基数的个数是无穷的。然而有趣的是，无穷基数的个数比任何基数都多，从而它是一个比任何无穷大都要大的“无穷大”，它不能对应于一个基数，否则会产生康托尔悖论的一种形式。

参考资料：百度百科---无穷大