用Mathematica研究曲线论（二）

1、求双曲螺旋r[t_]:={Cosh[t],Sinh[t],t}从t=0起计算的弧长。r[t_]:={Cosh[t],Sinh[t],t}ParametricPlot3D[r[t],{t,0,2 Pi}]ArcLength[r[t],{t,0,t}]

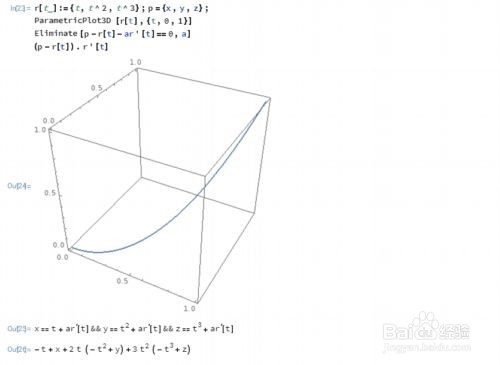
2、三次挠曲线r[t_]:={t,t^2,t^3}的切线和法平面方程。r[t_]:={t,t^2,t^3};p={x,y,z};ParametricPlot3D[r[t],{t,0,1}]Eliminate[p-r[t]-ar'[t]==0,a](p-r[t]).r'[t]

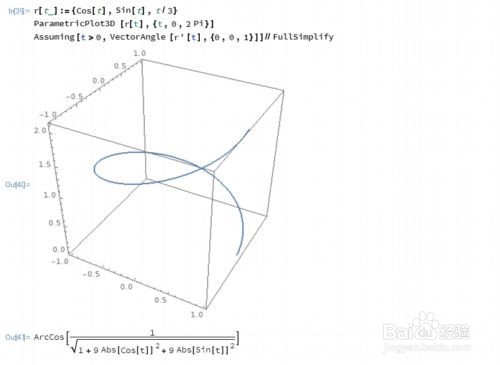
3、求证：圆柱螺旋r[t_]:={Cos[t],Sin[t],t}的切线和z轴夹角成定值。r[t_]:={Cos[t],Sin[t],t/3}ParametricPlot3D[r[t],{t,0,2 Pi}]Assuming[t>0,VectorAngle[r'[t],{0,0,1}]]//FullSimplify

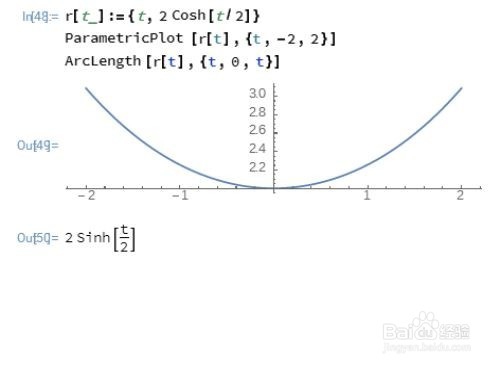
4、q求悬链线r[t_]:={t,2 Cosh[t/2]}从t=0起计算弧长。r[t_]:={t,2 Cosh[t/2]}ParametricPlot[r[t],{t,-2,2}]ArcLength[r[t],{t,0,t}]

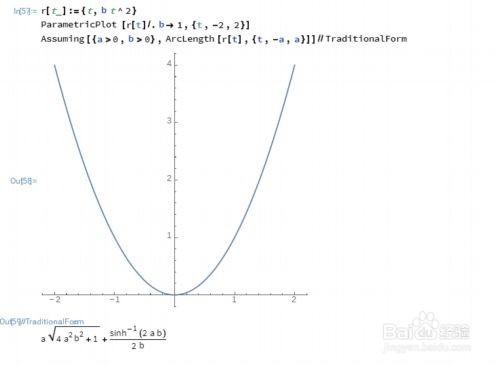
5、求抛物线y=x^2在区间[-a,a]之间的弧长。r[t_]:={t,b t^2}ParametricPlot[r[t]/.b->1,{t,-2,2}]Assuming[{a>0,b>0},ArcLength[r[t],{t,-a,a}]]//TraditionalForm

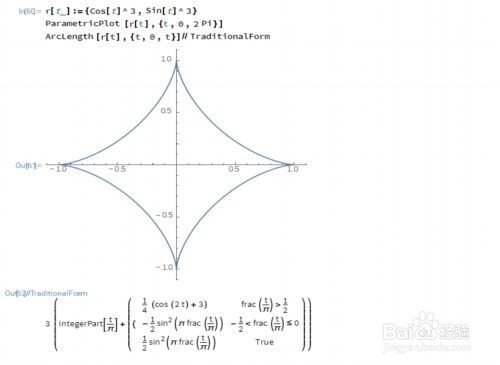
6、求星形线r[t_]:={Cos[t]^3,Sin[t]^3}的弧长。r[t_]:={Cos[t]^3,Sin[t]^3}ParametricPlot[r[t],{t,0,2 Pi}]ArcLength[r[t],{t,0,t}]//TraditionalFormArcLength[r[t],{t,0,2 Pi}]//TraditionalForm

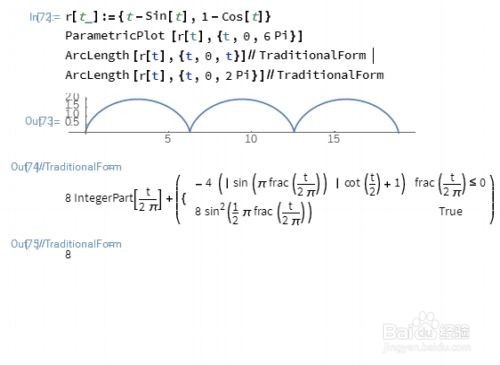
7、求旋轮线r[t_]:={t-Sin[t觥终柯计],1-Cos[t]}在区间【0，2π】之间的弧长。r[t_]:={t-Sin[t],1-Cos[t]}ParametricPlot[r[t],{t,0,6 Pi}]ArcLength[r[t],{t,0,t}]//TraditionalFormArcLength[r[t],{t,0,2 Pi}]//TraditionalForm

8、求曲线｛x^3==3 a^2 y,2 垓矗梅吒x z==a^2｝在平面y=a/3和平面y=9 a之间的弧长。当y=a/3时，x=a；当y=9 a时，x=3 a；r[x_]:={x,(x^3)/(3 a^2),(a^2)/(2 x)}ParametricPlot3D[r[x]/.a->1,{x,1,3}]ArcLength[r[x],{x,a,3 a}]//TraditionalForm

9、把圆柱螺旋r[t_]:={a Cos[t],a Sin职邗珩垃[t],b t} 化为自然参数方程的形式。r[t_]:={a Cos[t],a Sin[t],b t}ArcLength[r[t]荑樊综鲶,{t,0,t}]//TraditionalForm然后，{a Cos[t],a Sin[t],b t} /.t->s/Sqrt[a^2+b^2]检测一下：r[s_]:={a Cos[t],a Sin[t],b t} /.t->s/Sqrt[a^2+b^2]r[s]r'[s]r'[s].r'[s]r'[s].r'[s]//FullSimplify