蒙日圆定理证明是怎么样的

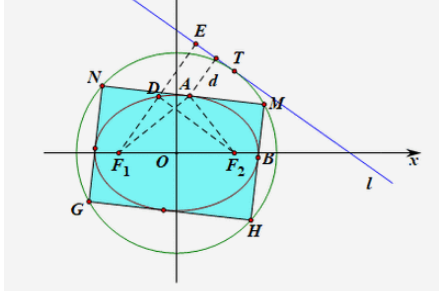
蒙日癣嗡赧箬圆定理是任意两条互相垂直的切线的交点都在同一个圆上，它的圆心是椭圆（双曲线）的中心，喊岭谎儿半径等于长半轴（实半轴）与短半轴（虚半轴）平方和（差）的算术平方根，这个圆叫蒙日圆。

过圆锥曲线外一点作两条互相垂直的切线，那么这一点的轨迹是一个圆，这个圆被称为蒙日圆，又叫外准圆。

圆的特殊性：

1、圆周率实验在圆形纸片上做个记号，与直尺0刻度对齐，在直尺上滚动一周，求出圆的周长。发现一般规律，就是圆周长与它直径的比值是一个固定数(π)。

3、圆周率任意一个圆的周长与它的直径的比值是一个固定的数，我们把它叫作圆周率。用字母π(pai) 表示。

4、一个圆的周长总是它直径的3倍多一些，这个比值是一个固定的数。圆周率π是一个无限不循环小数。在计算时，一般取π ≈ 3.14。

5、在判断时，圆周长与它直径的比值是π倍，而不是3.14倍。世界上第一个把圆周率算出来的人是我国的数学家祖冲之。