用Mathematica求图像的共生矩阵

1、给出下面的图片。上面的图片是下面的图片的3000*3000的共生矩阵对应的像素图增亮16000倍的效果。

2、查看图片尺寸：{u, v} = ImageDimensions[b]

3、图像数据：c = Floor[#*10]/10. & /@ ImageData[b]

4、从c的第二列数据开始，每个像素撕良滤儆值与它左面那个像素值合成一对：d = Table[{c[[m, n]], c[[m, n - 1]]}, {m, 1, v}, {n, 2, u}] // 僻棍募暖Flatten[#, 1] &;

5、数一数{0.,0.}在d里面出现的次数：Count[d, {0., 0.}]进而算出{0.,0.}在d里面出现的概率：Count[d, {0., 0.}]/Length[d]*1.

6、{0., 0.1, 0.2, 0.3, 0.4, 0.5巳呀屋饔, 0.6, 0.7, 0.8, 0.9}，允许重复的两两配对，一共可以有100种情形。考虑这100种情形，在d里面出现的概率：e = Table[Count[d, {i, j}/10.]/Length[d], {i, 0, 9}, {j, 0, 9}];这个e就是原图的10*10的共生矩阵。注意，看下图矩阵：左上角的数值，代表{0.,0.}在d里面出现的概率；右下角的数值，代表{0.9,0.9}在d里面出现的概率。

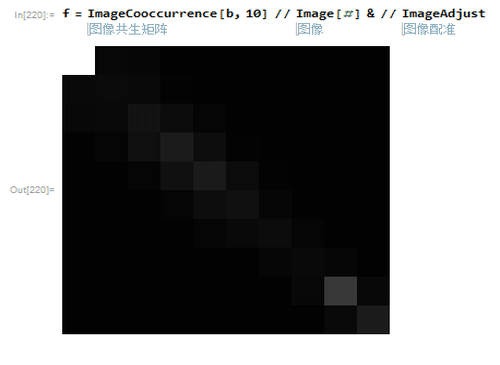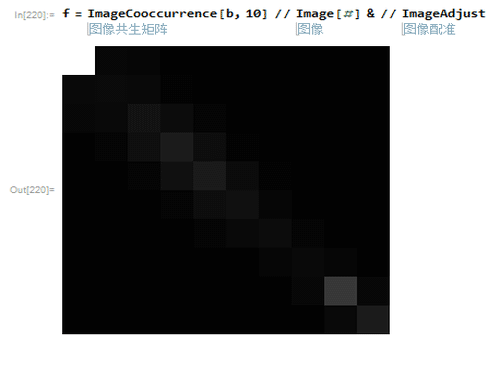
7、下图是共生矩阵e的像素图。越亮，代表这个位置出现的概率越大。

8、上面求共生矩阵的步骤，在Mathematica里面，整合成了一个函数：e=ImageCooccurrence[b, 10]

9、100*100的共生矩阵：ImageCooccurrence[b, 100]下图是对应的像素图增亮600倍的效果。