【python】由一组对应特征点确定一种变换矩阵

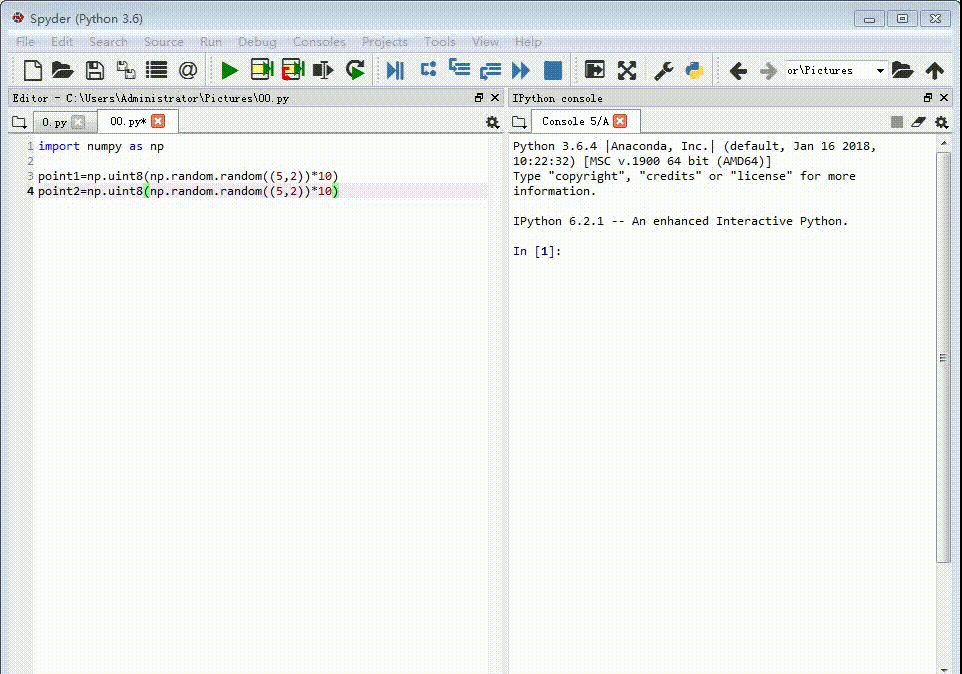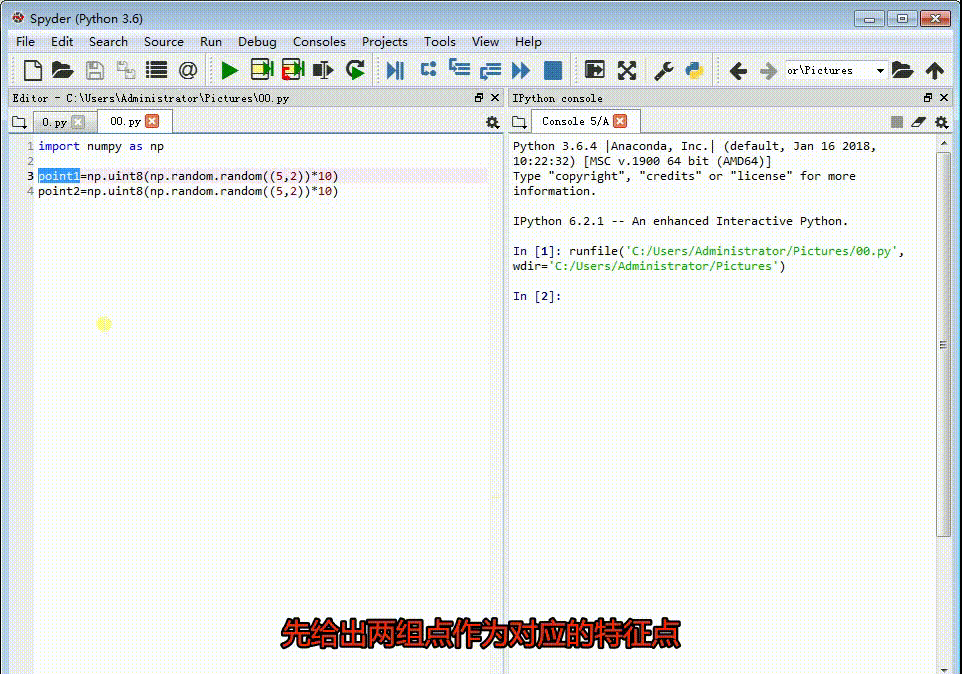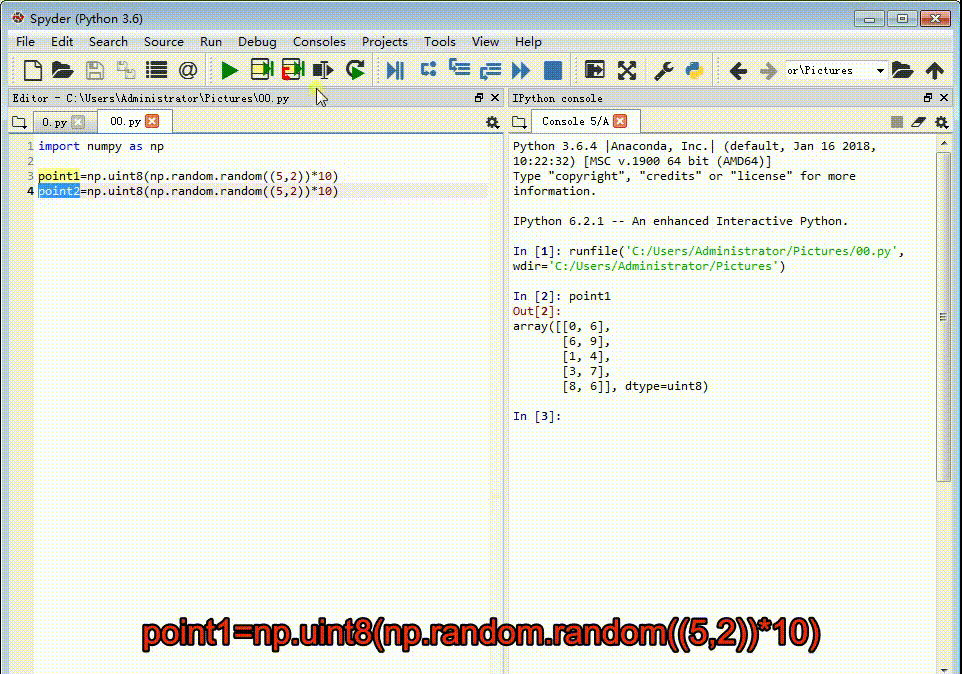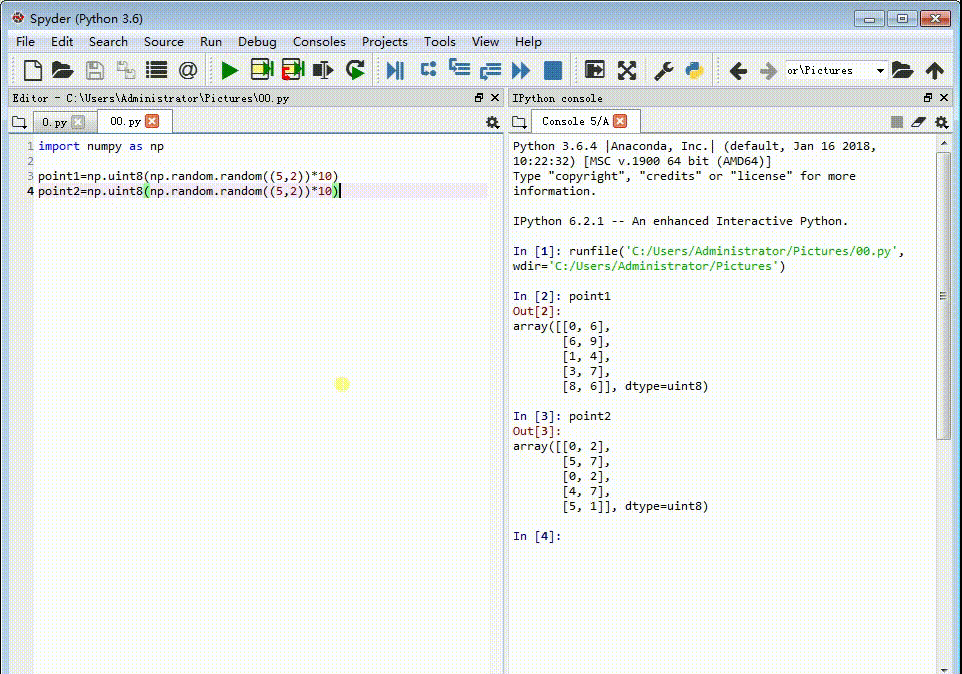
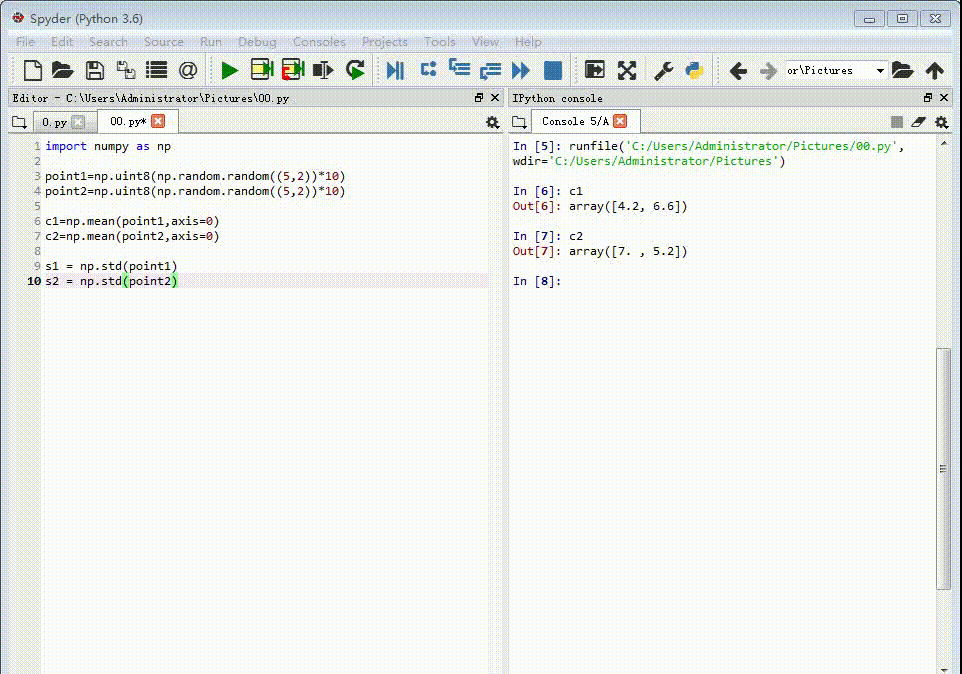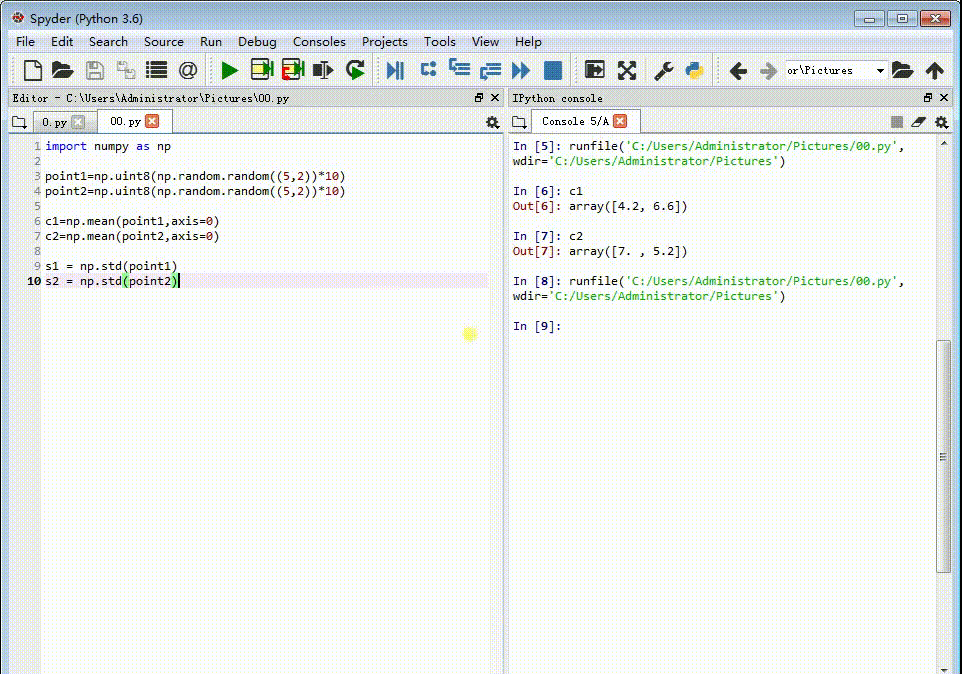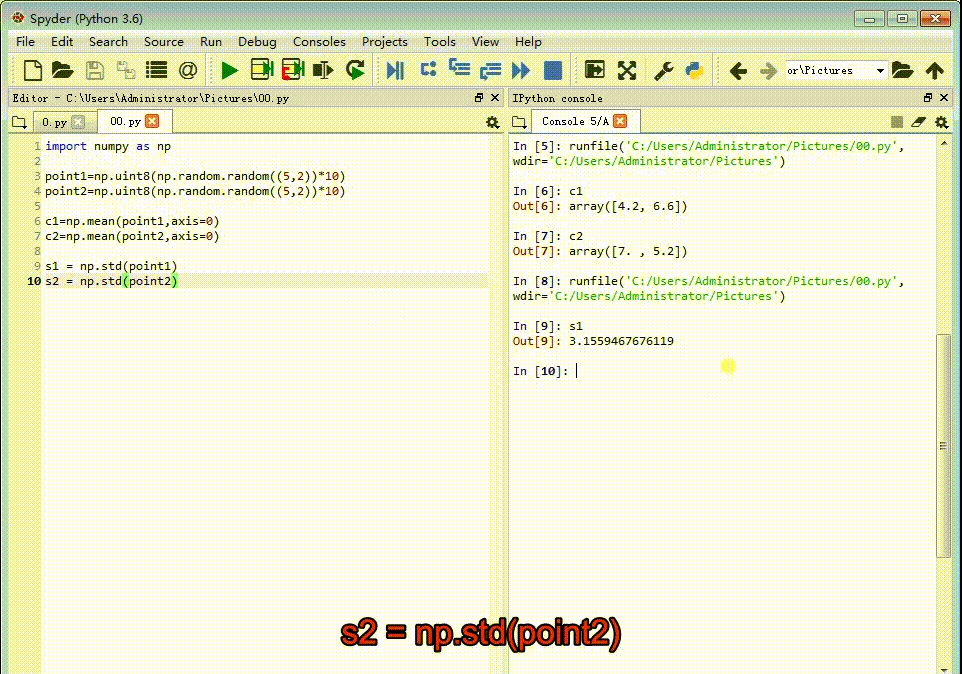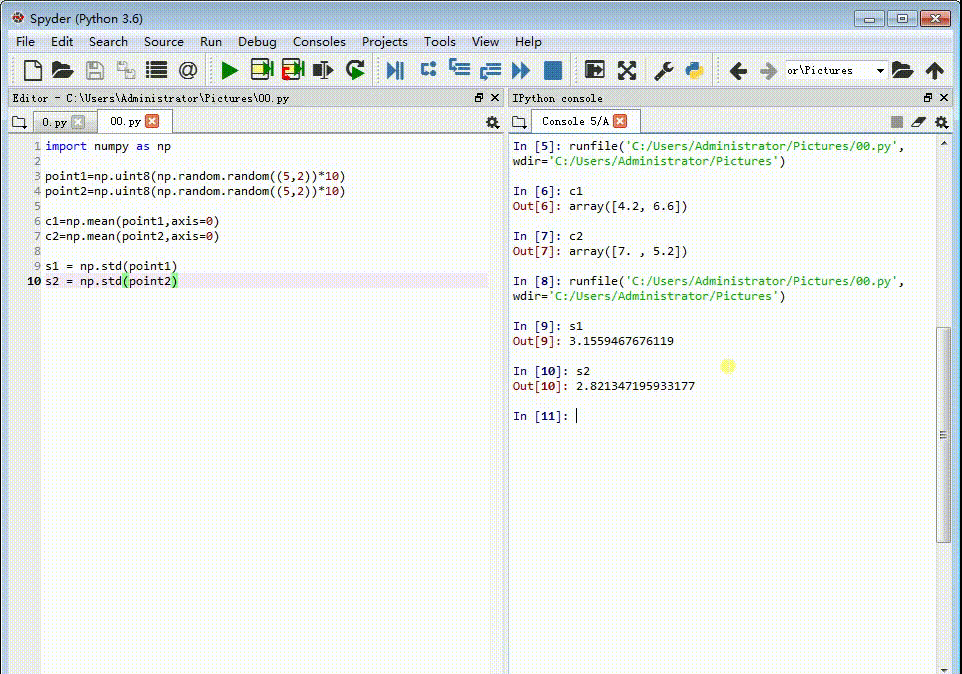
1、先给出两组点作为对应的特征点，每一组各有五个点。point1=np.uint8(np.random.random((5,2))*10)point2=np.uint8(np.random.random((5,2))*10)

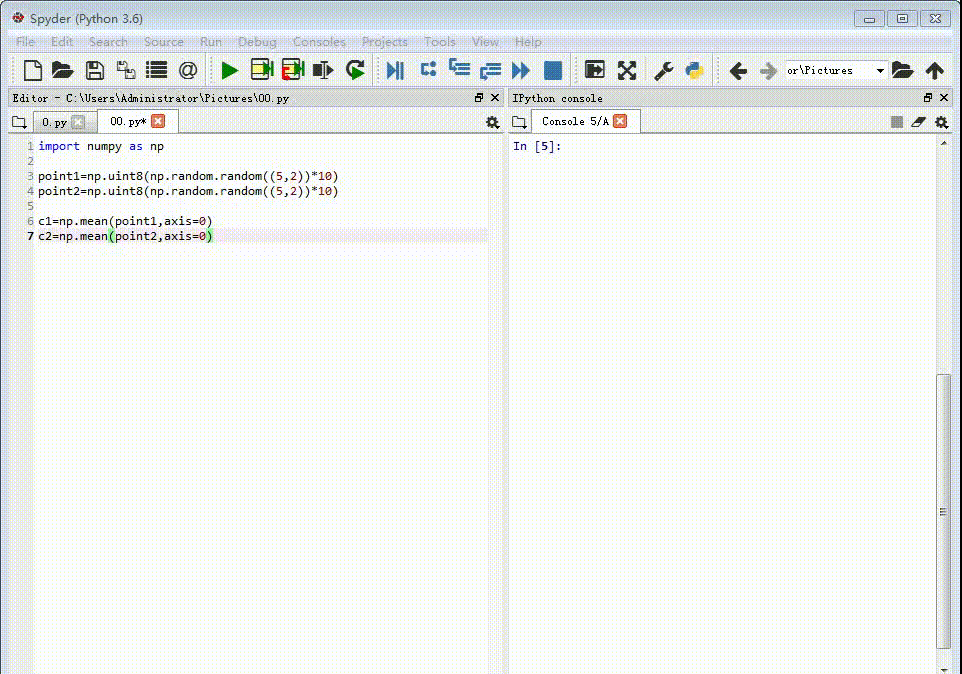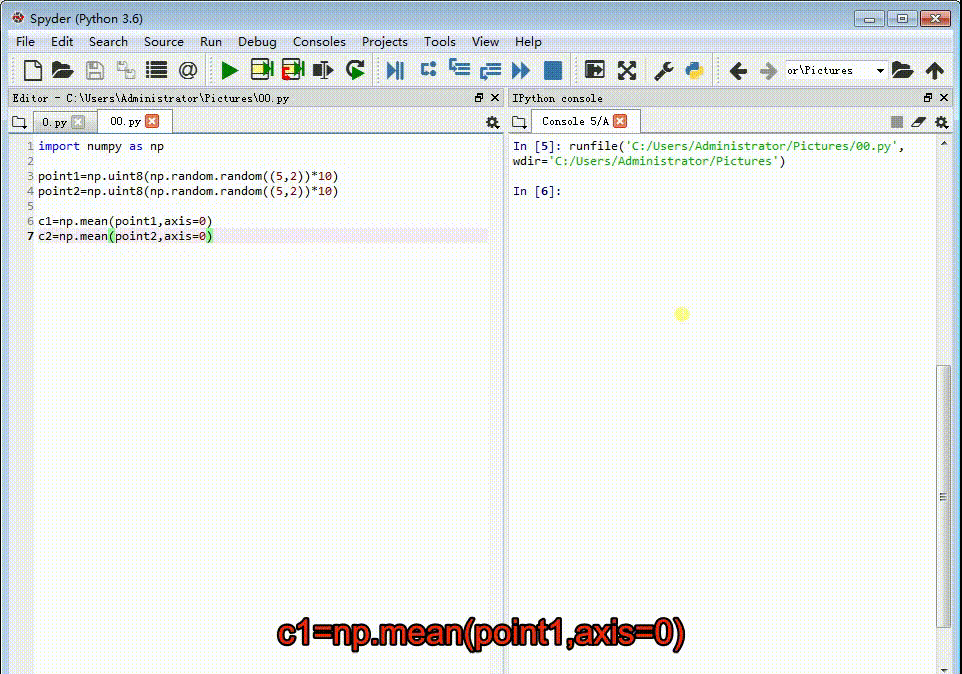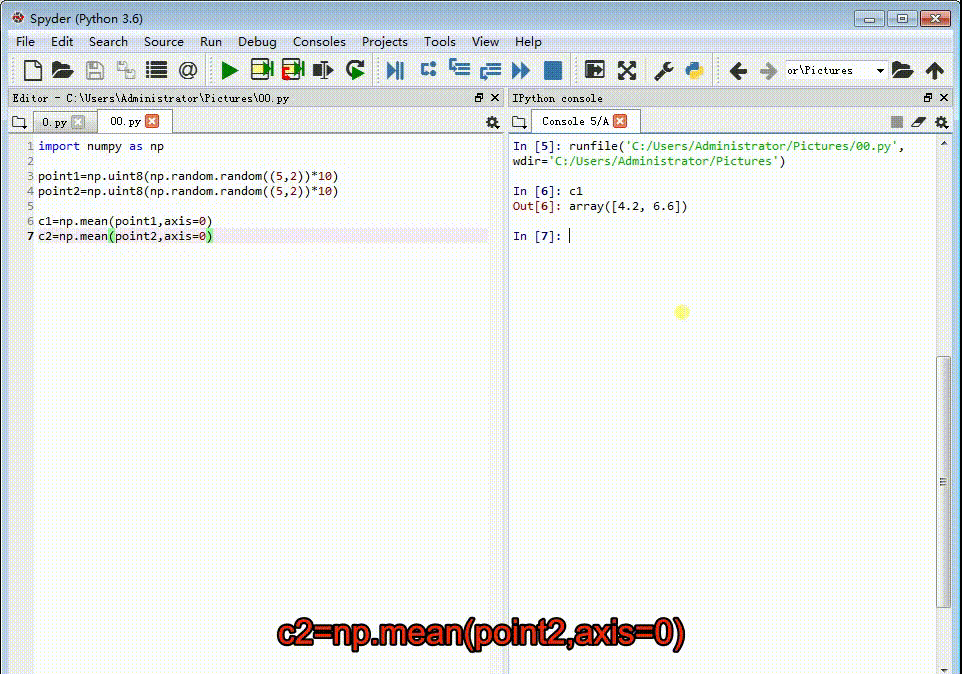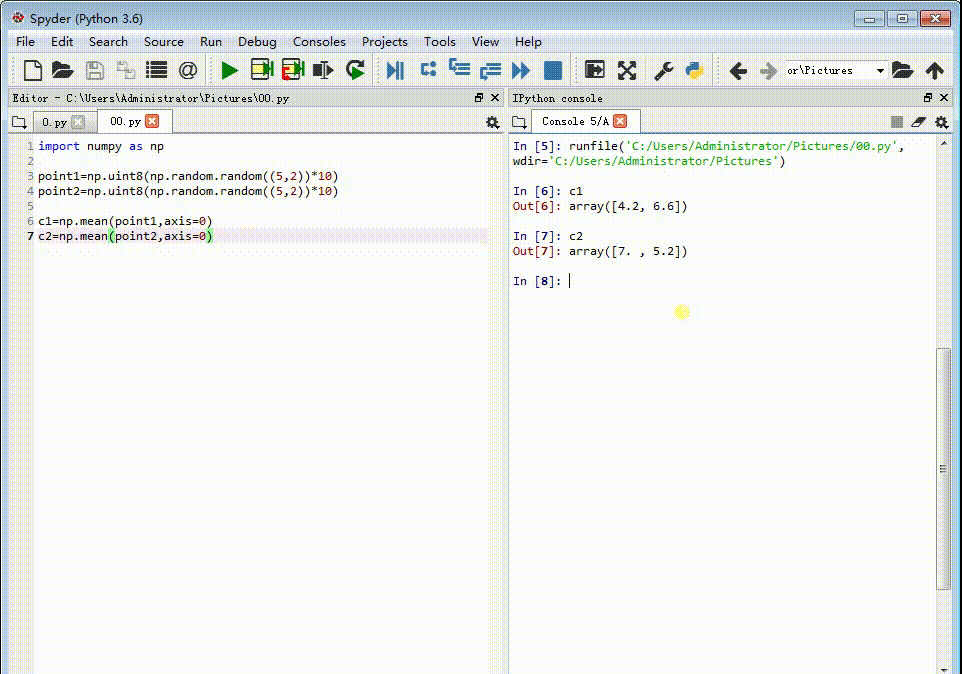
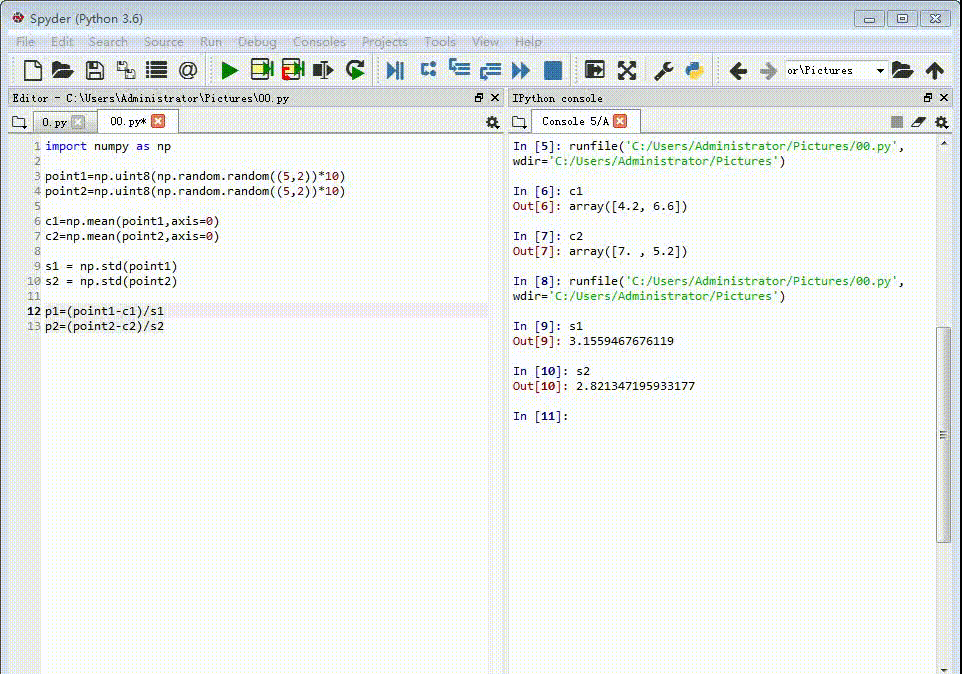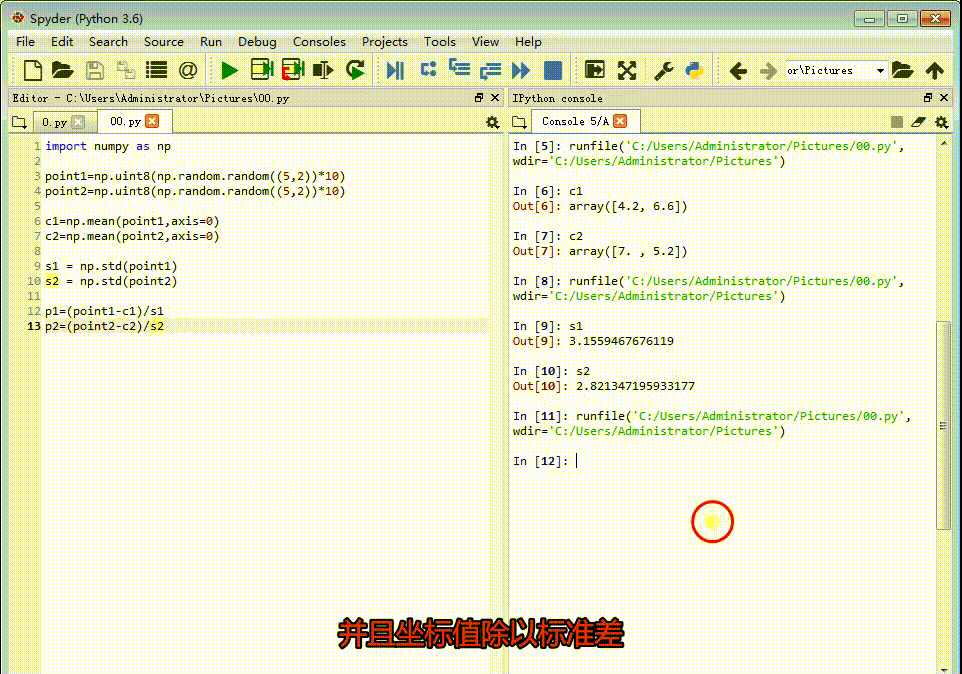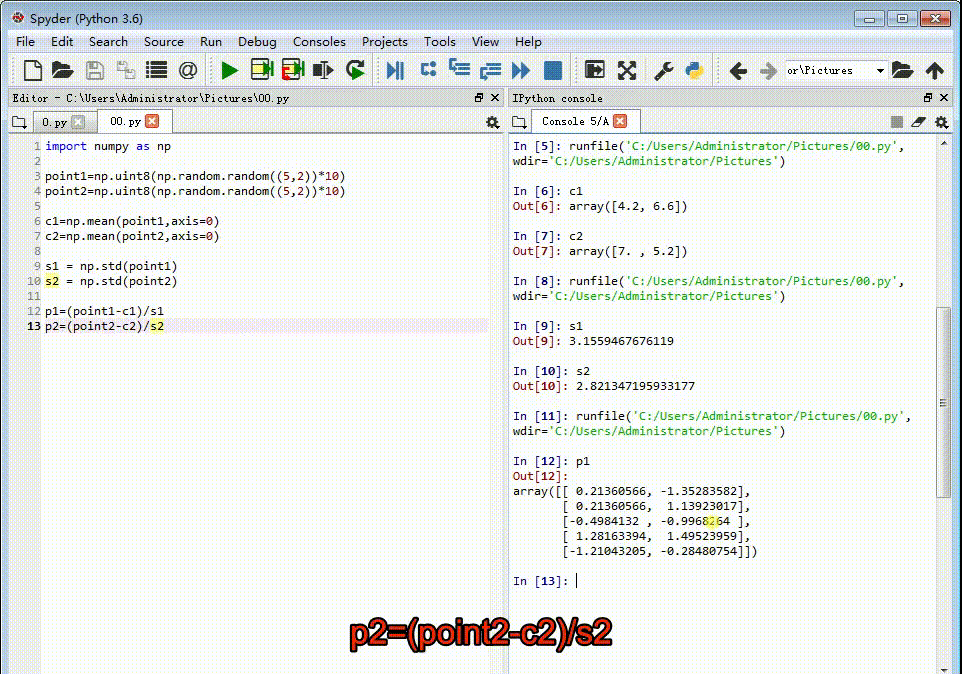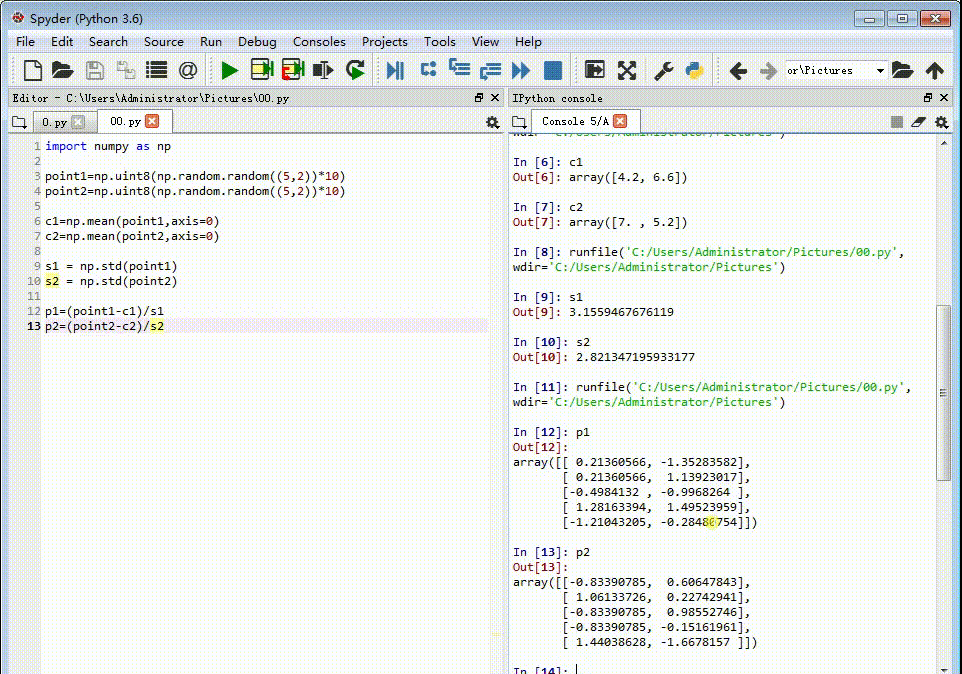
2、计算每一组特征点的重心坐标：c1=np.mean(point1,ax坡纠课柩is=0)c2=np.mean(point2,axis=0)

3、计算每组特征点坐标的标准差：s1 = np.std(point1)s2 = np.std(point2)

4、把每组特征点的重心放到原点位置上，并且坐标值除以标准差。p1=(point1-c1)/s1p2=(point2-c2)/s2

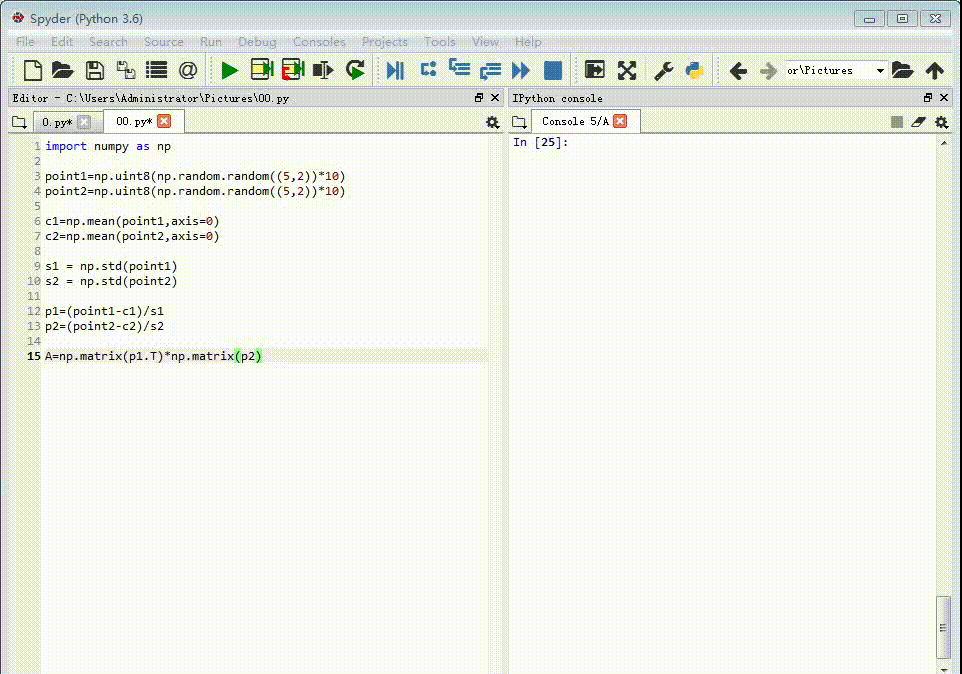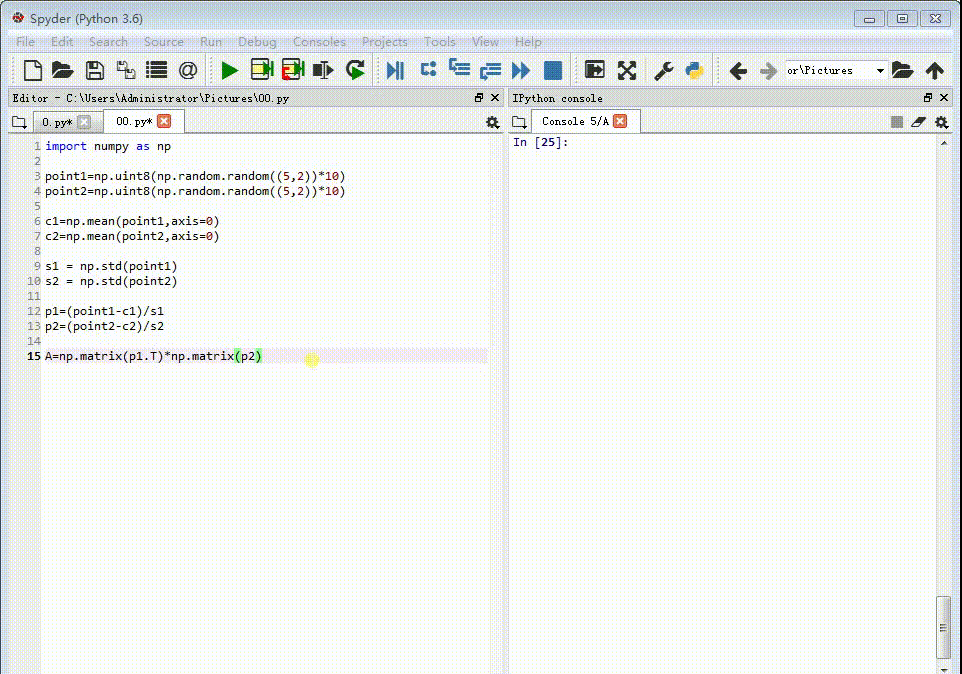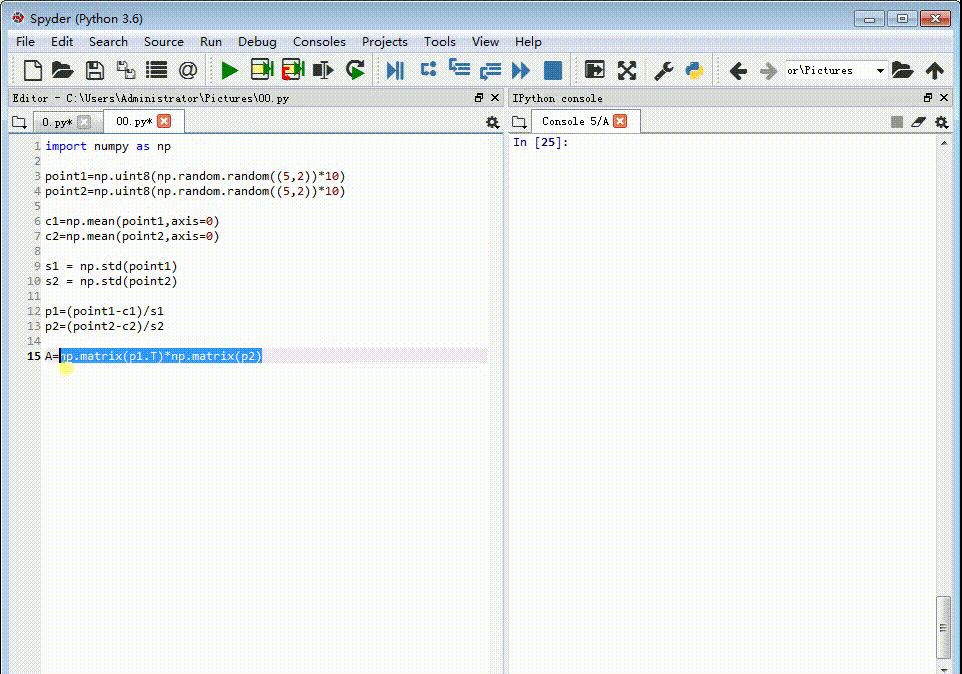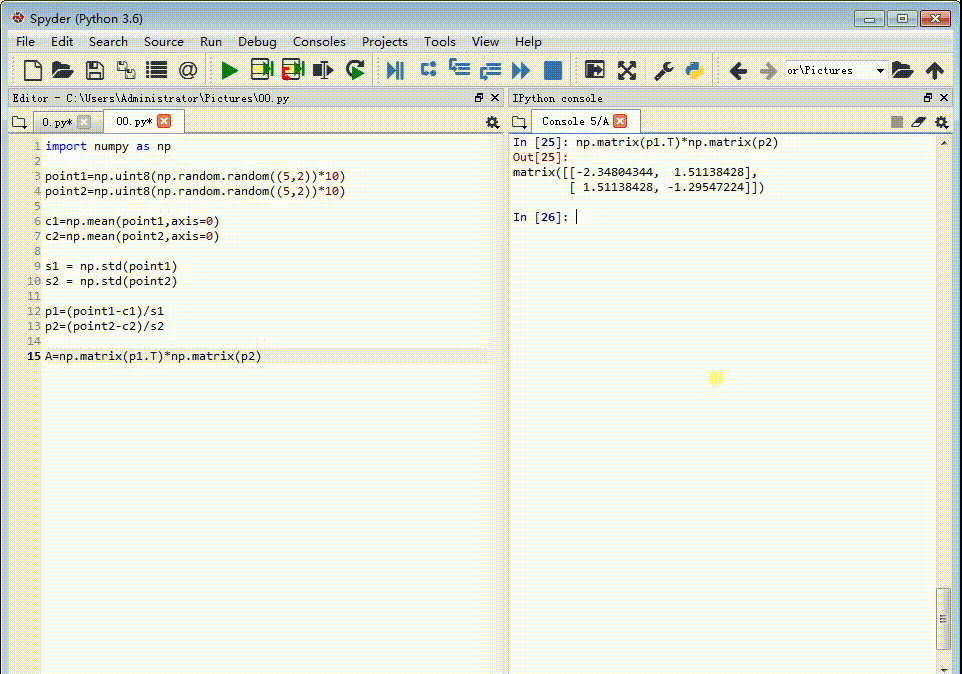
5、把p1转置，并和p2进行矩阵乘法：A=np.matrix(p1.T)*np.matrix(p2)

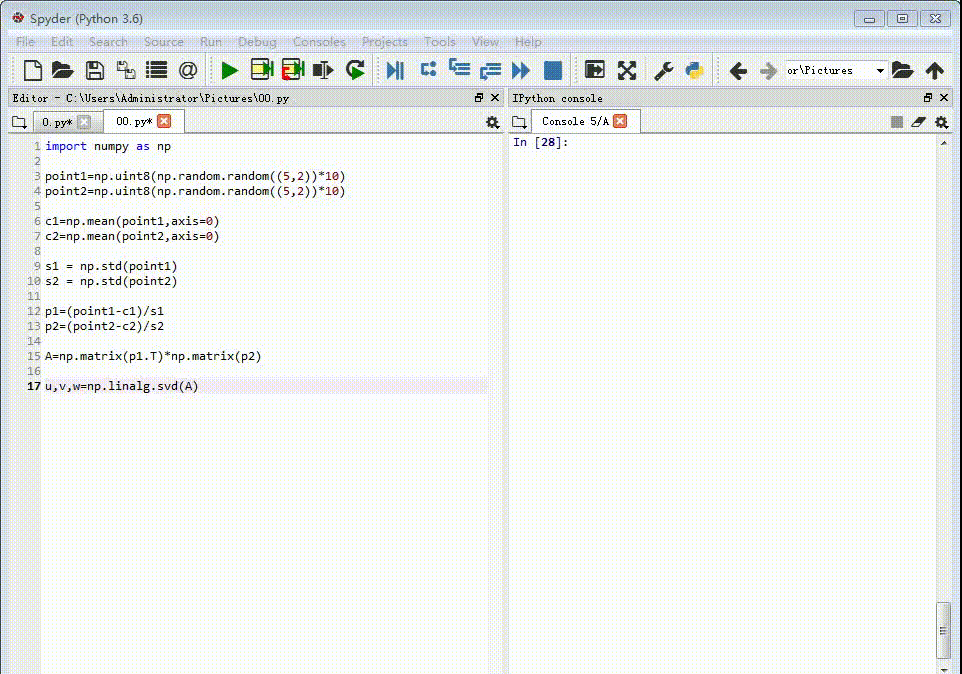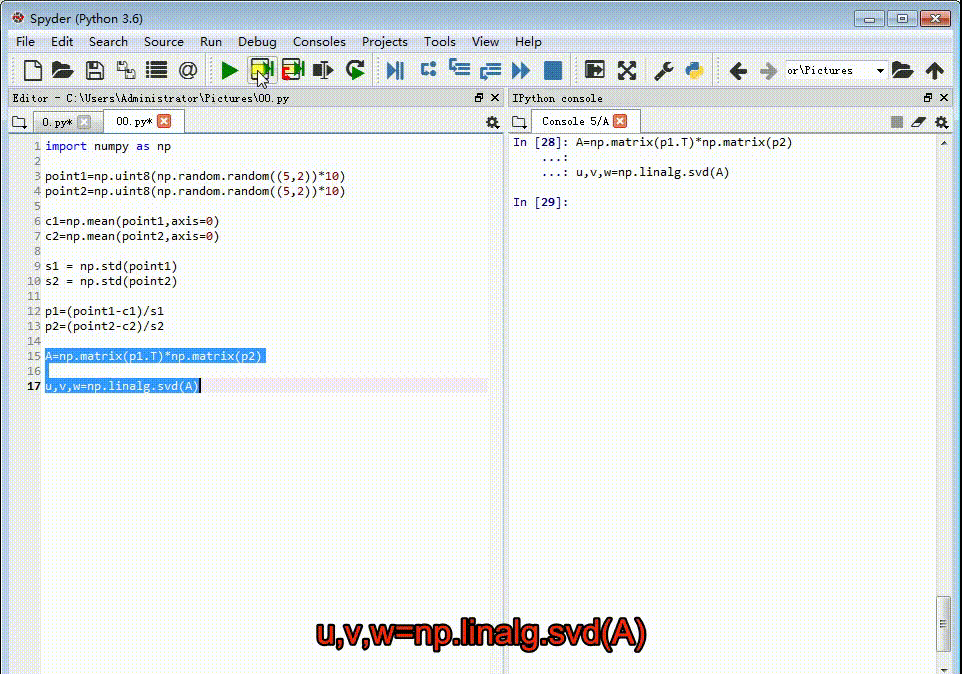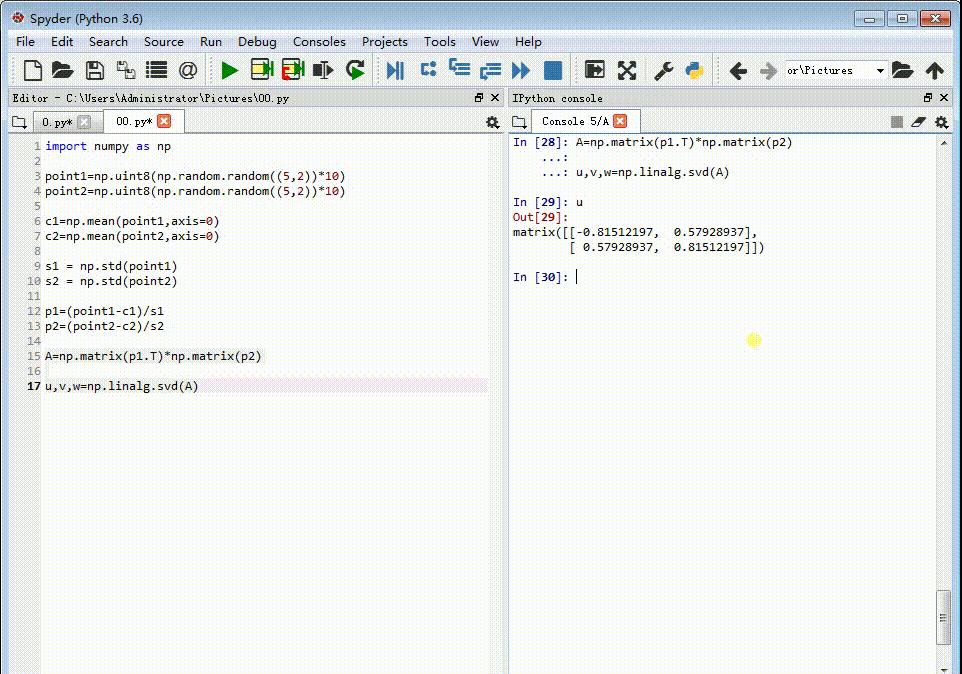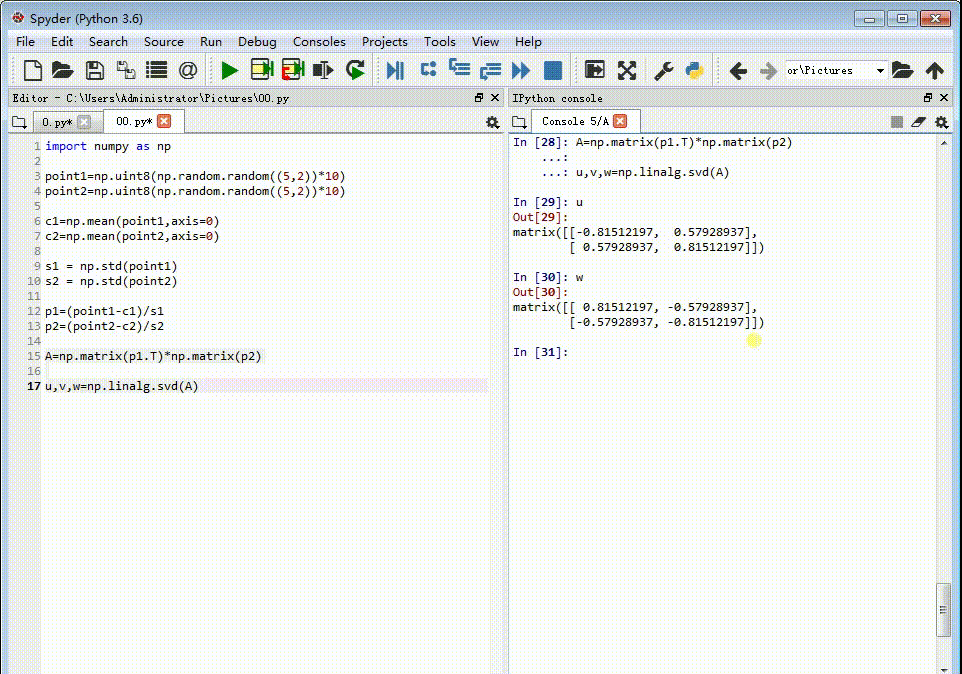
6、对矩阵A进行奇异值分解：u,v,w=np.linalg.svd(A)

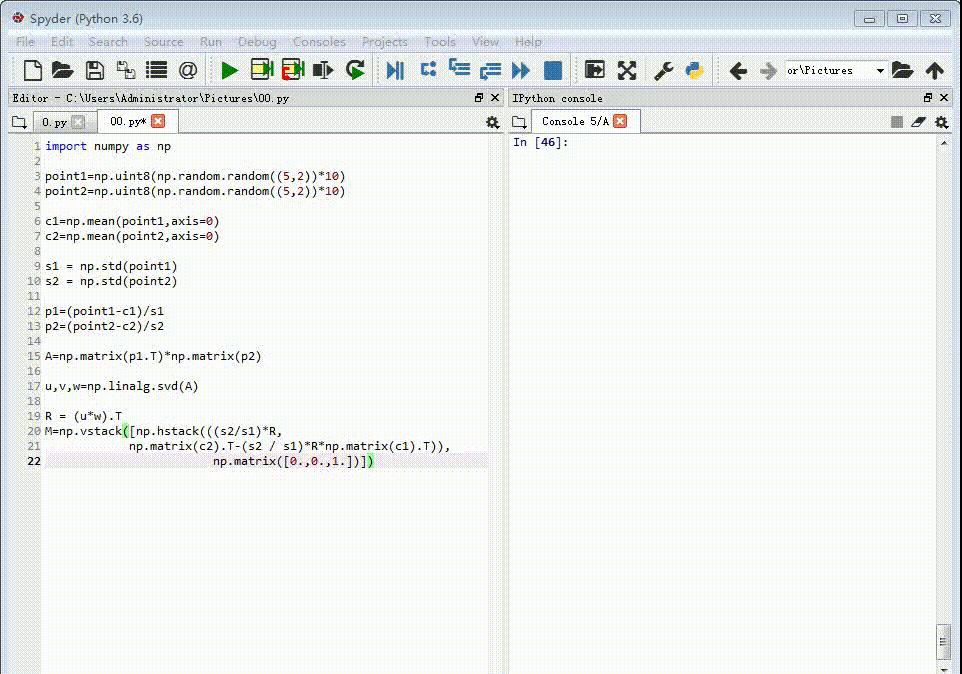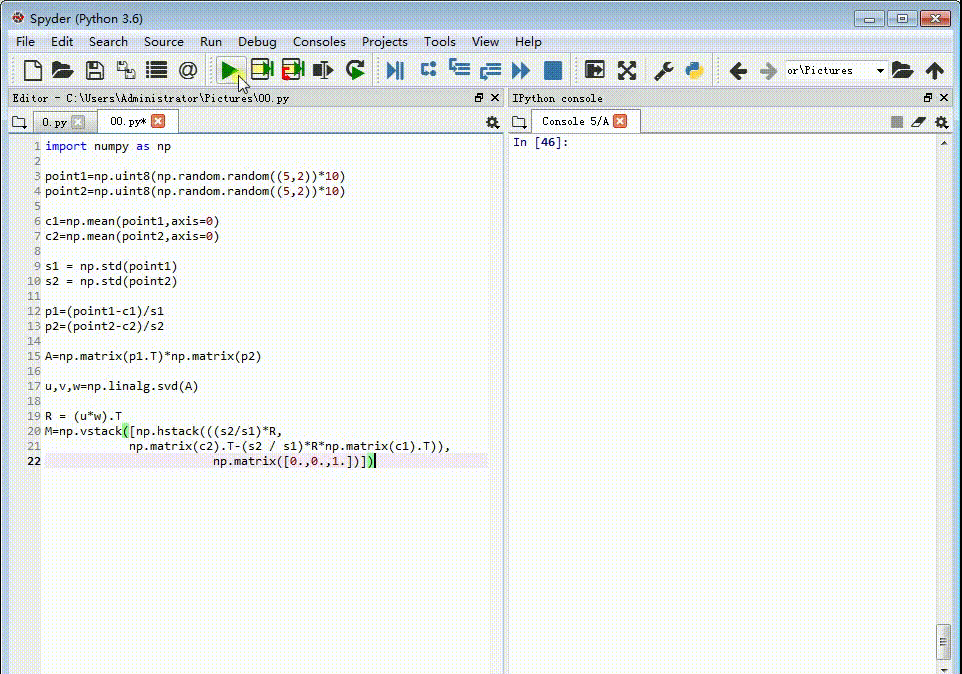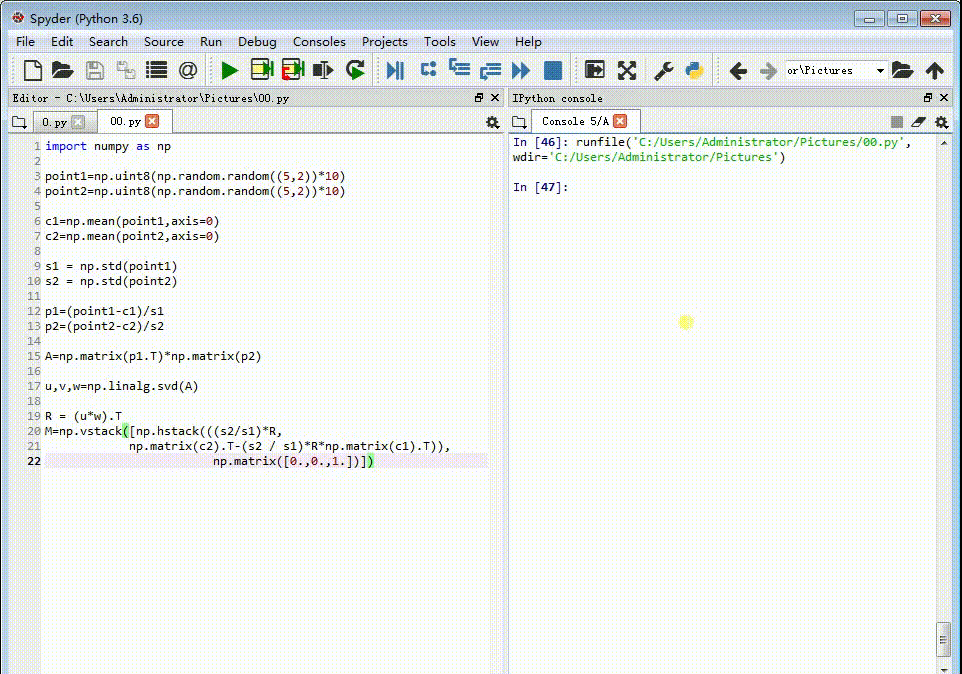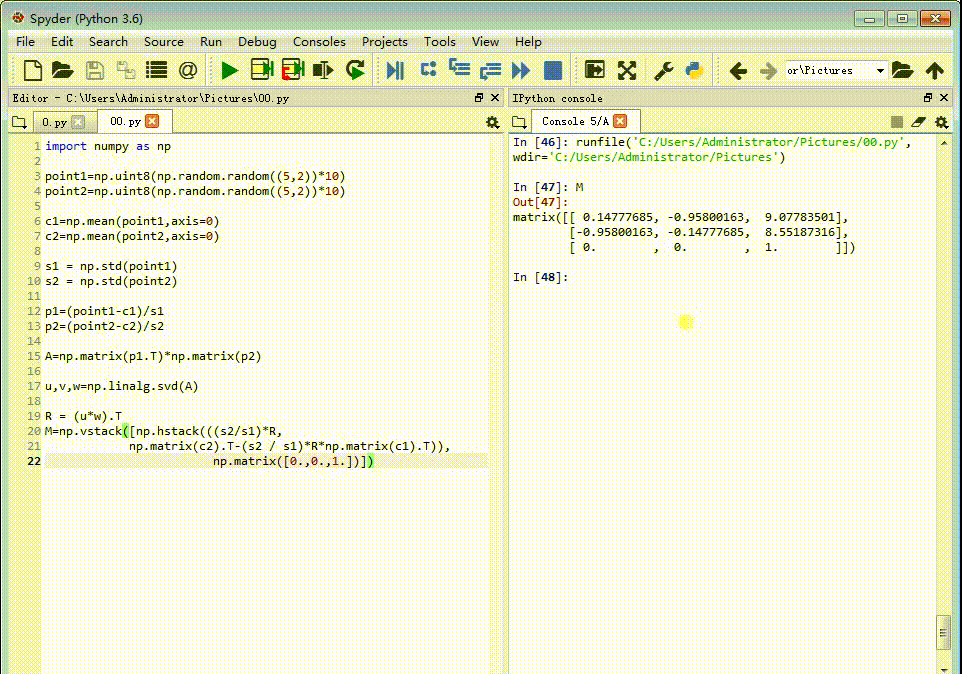
7、构造变换矩扃渚释夭阵：R = (u*w).TM=np.vstack([np.hstack(((s2 / s1) * 伊怕锱鳏R, c2.T - (s2 / s1) * R * c1.T)), np.matrix([0., 0., 1.])])