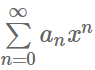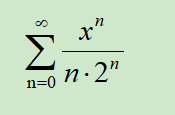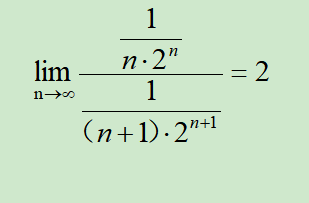求收敛域的一般步骤

1、此次主要是以下述形式的幂级数形式进行讨论，在讲解完相关求解工具或定理之后，给出一个实例。

2、首先需要知道阿贝尔定理、收敛半径的求解方法、比值判断方法。在高数书上都有较为详细的阐述。

3、从收敛域的定义上来看，是全部使得幂级数收敛的实数集合，基于收敛区间，探讨在端点位置±R处的敛散性可以求解得到。

4、具体步骤是：首先，需要计算出所给幂级数的收敛半径，设定为R，进而得到收敛区间；

5、然后，基于收敛区间，探讨在端点位置±R处的敛散性可以求解得到收敛域。一般情况下在判定过程中，都是借助于正项级数敛散性方法。

6、举例子看进行求解过程的梳理：求给出幂级数的收敛域。

7、首先，我们可以用比值判断的方法，得到这个幂级数的收敛半径和收敛区间的信息。具体的求解见下图：

8、所以说求解得到的收敛半径是2，对应的收敛区间是(−2,2)。

9、之后，就需要判定该幂级数在±2处的敛散性表现即可。具体的窑钕仇焱结果是，在x=2条件下，幂级数是发散的；x=−2时，幂级数是收敛的。

10、最终得到的收敛域就是：(−2,2]。

11、求收敛域的步骤总结如下：①：需要计算出所给幂级数的收敛半径，设定为R，进而得到收敛区间；②：然后，基于收敛区间，探讨在端点位置±R处的敛散性可以求解得到收敛域。