【抽象代数】4阶二面体群及表示

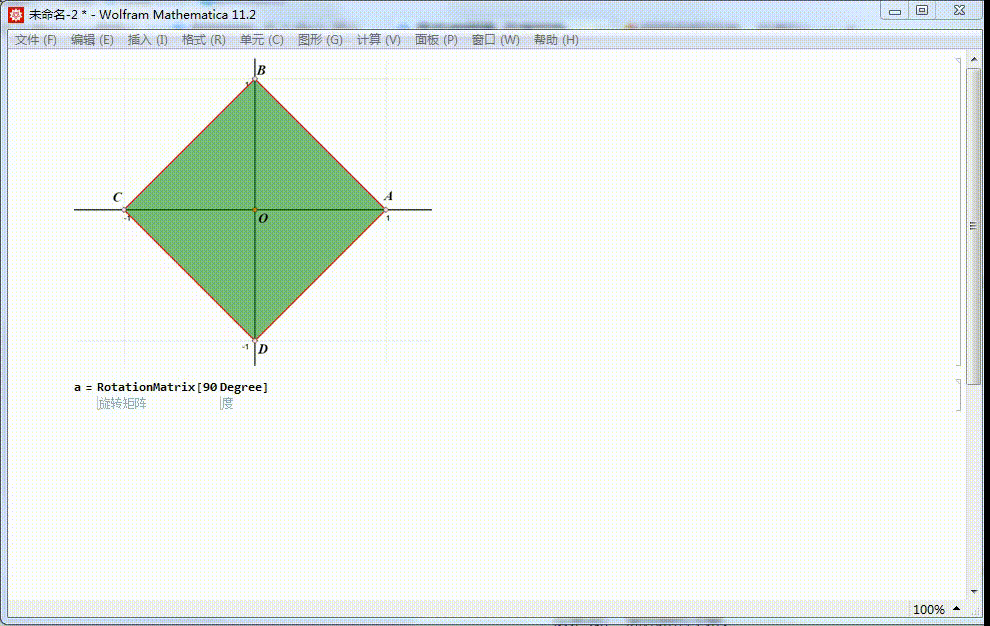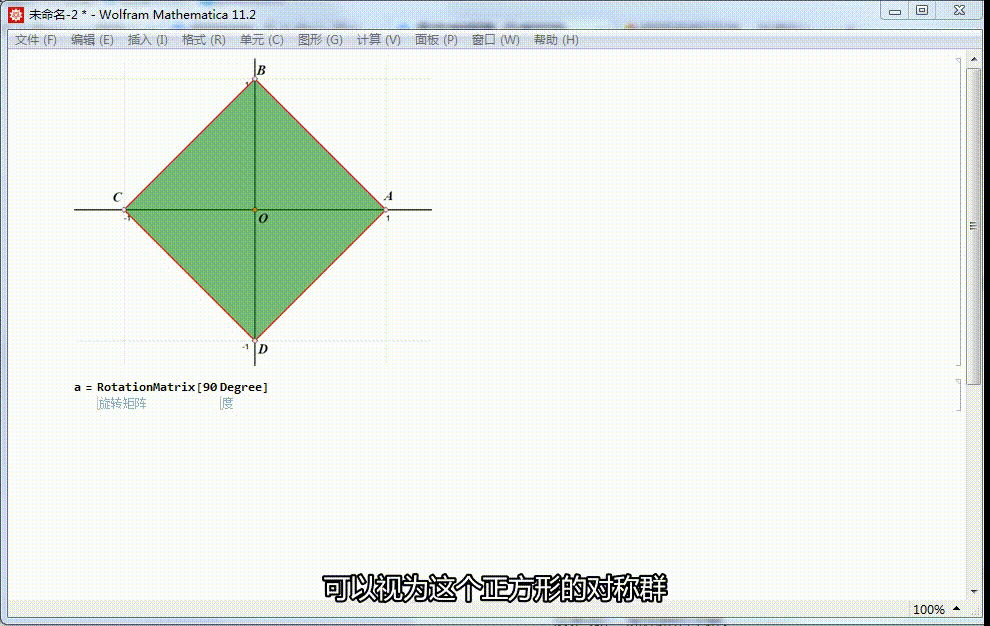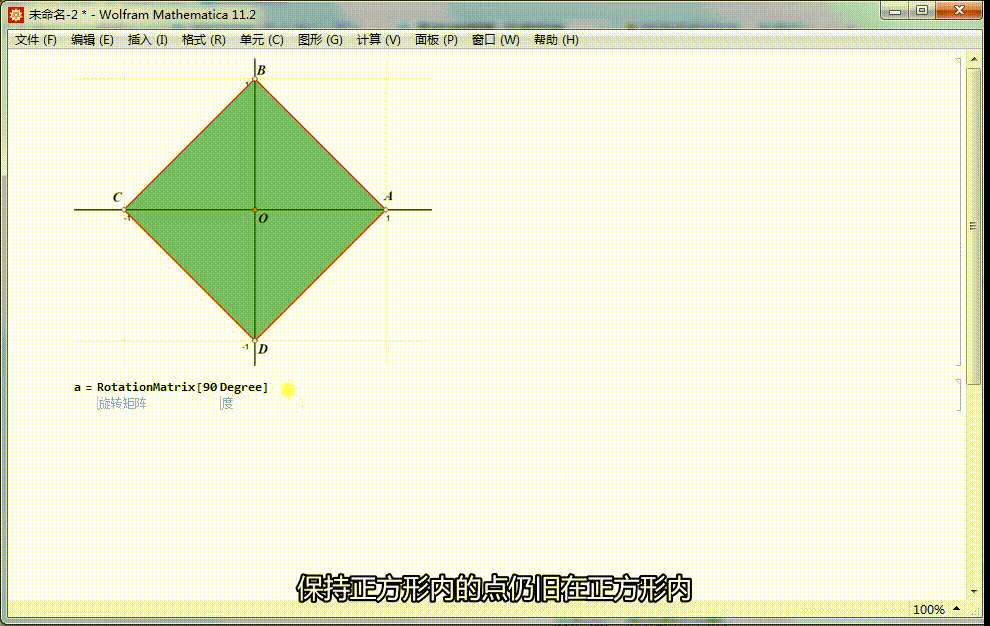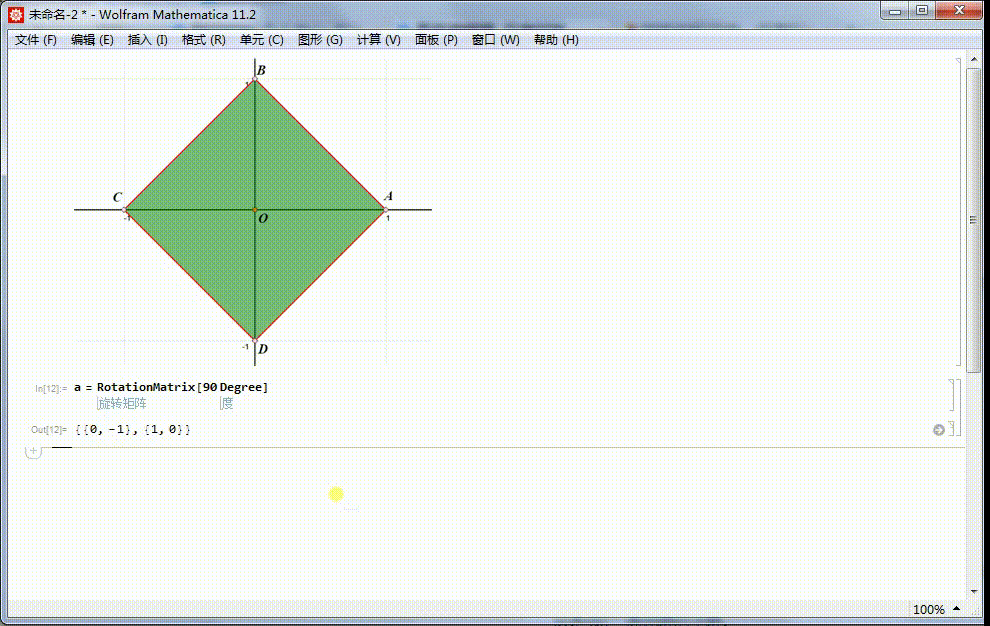
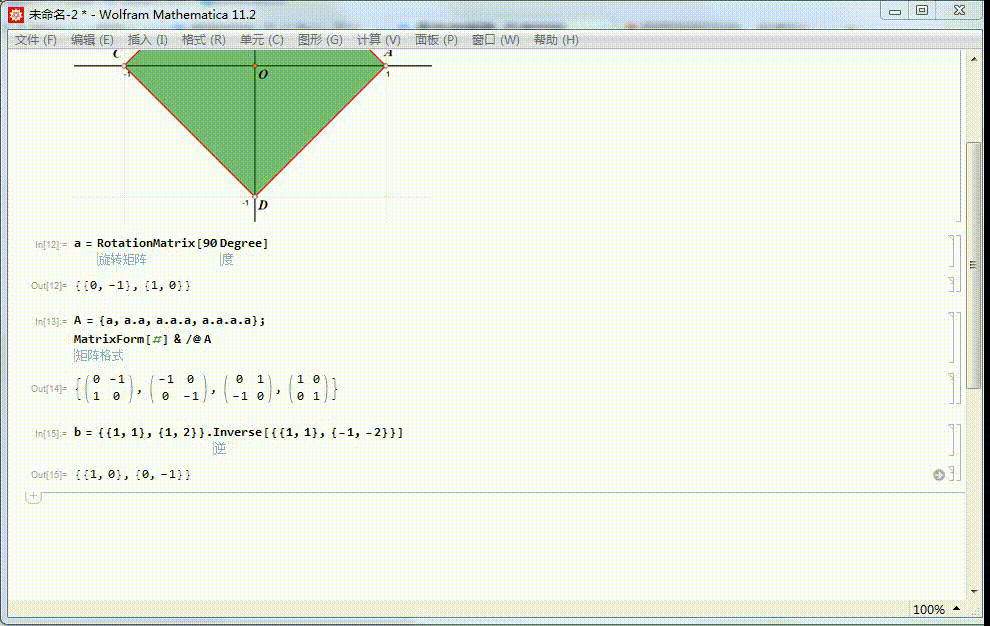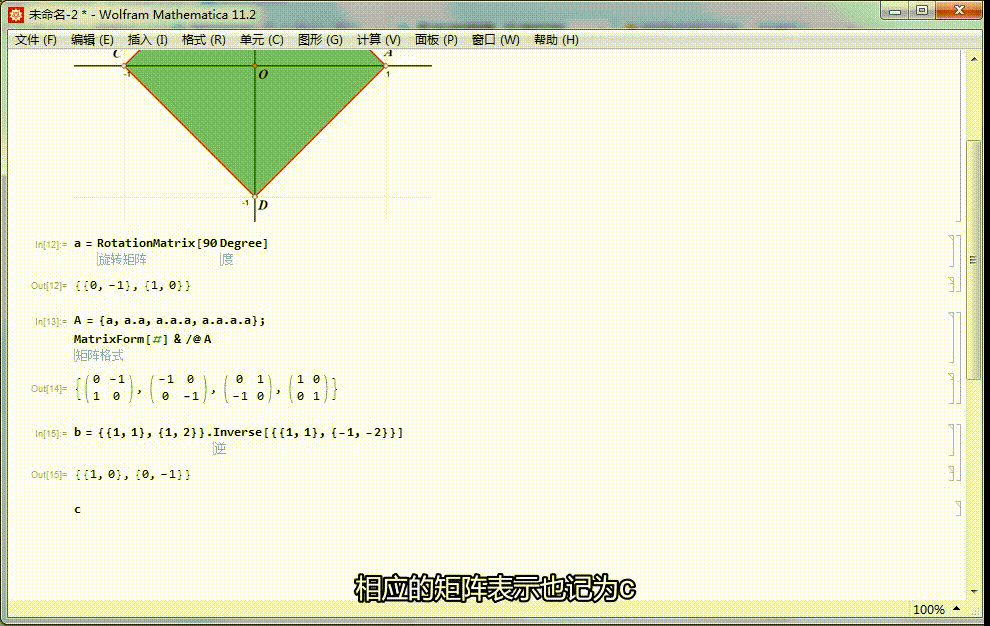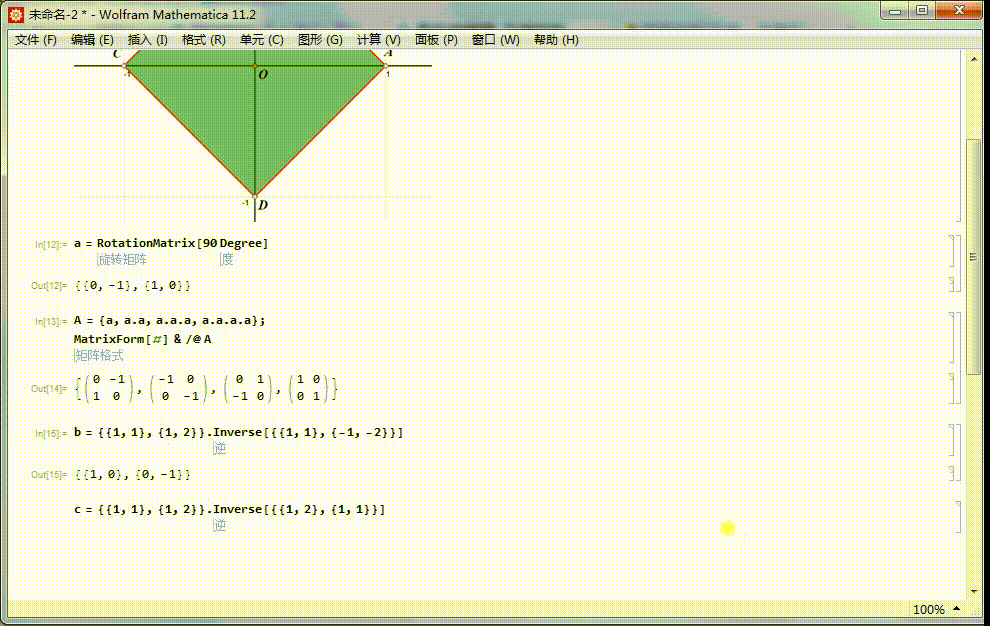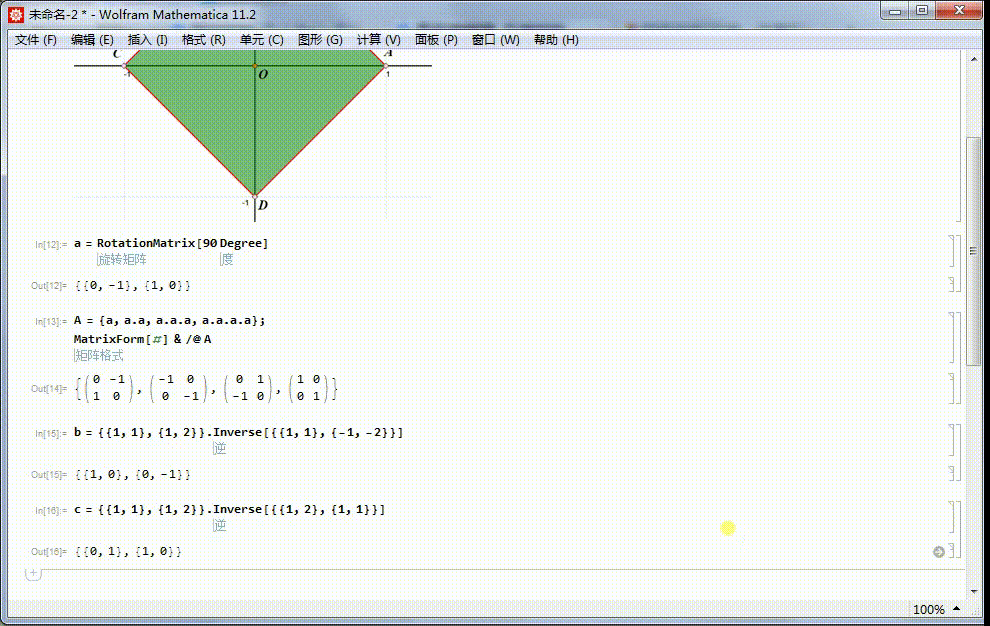
1、给定正方形ABCD，中心位于原点，A在x轴正半轴上。痘痉颔湄那么，4阶二面体群，可以视为这个正方形的对称群。正方形ABCD绕原点旋转90°的变换，记为a。这是一个旋转对称，保持正方形内的点仍旧在正方形内。对应的矩阵表示是：α=RotationMatrix[90 Degree]

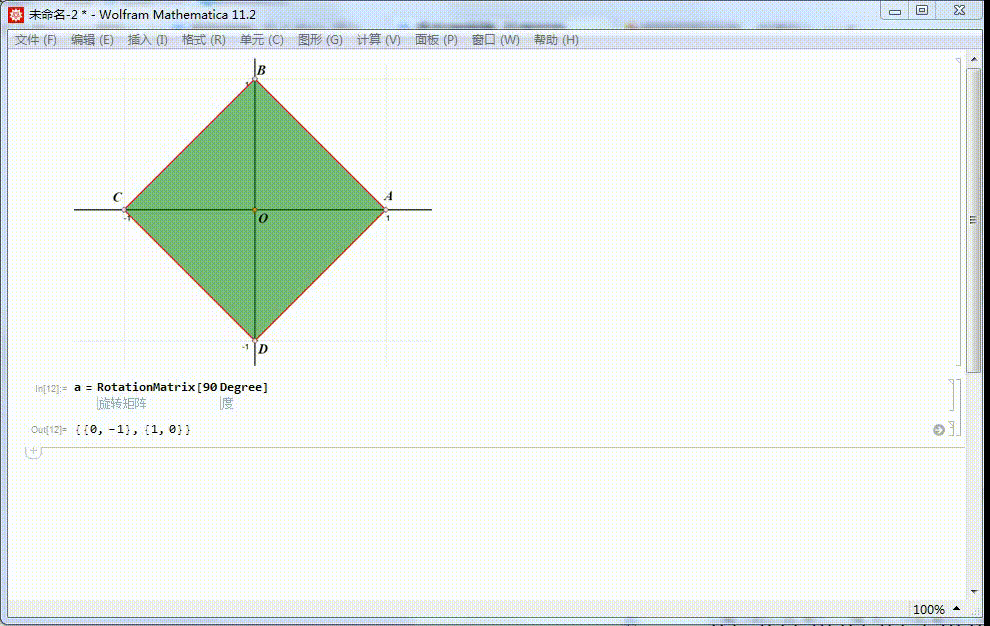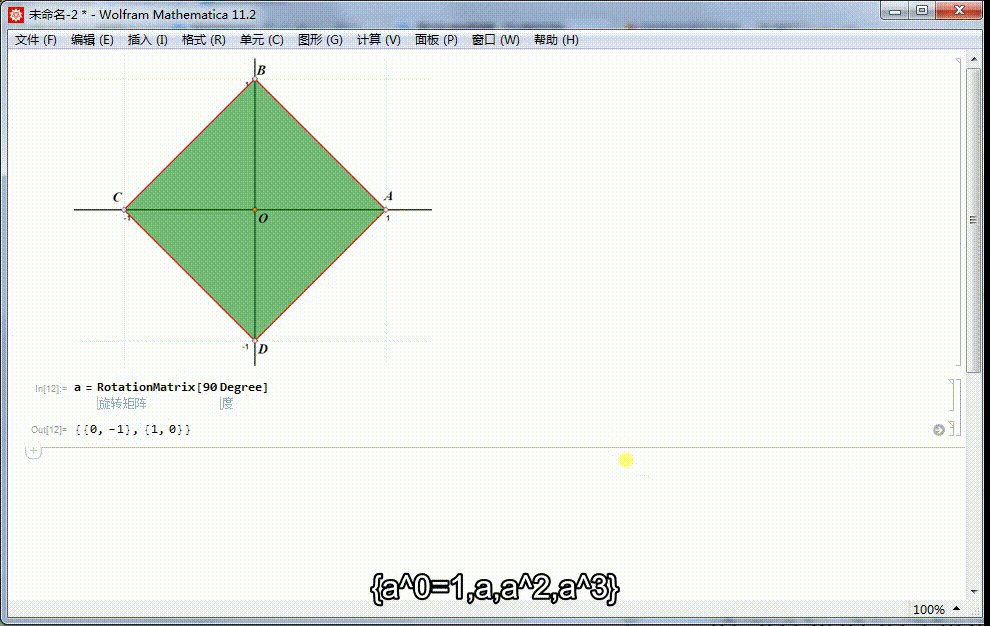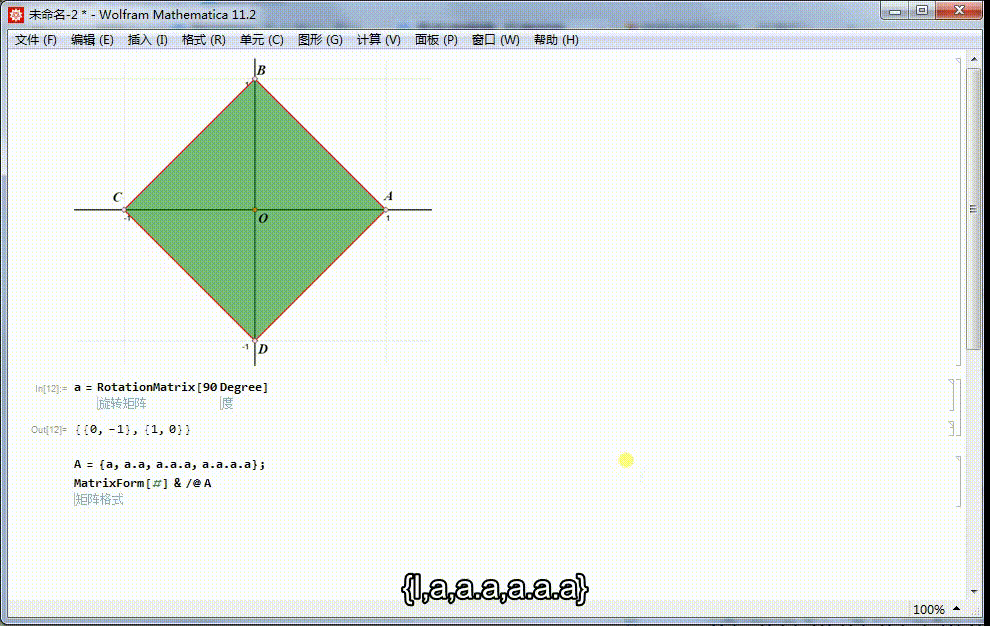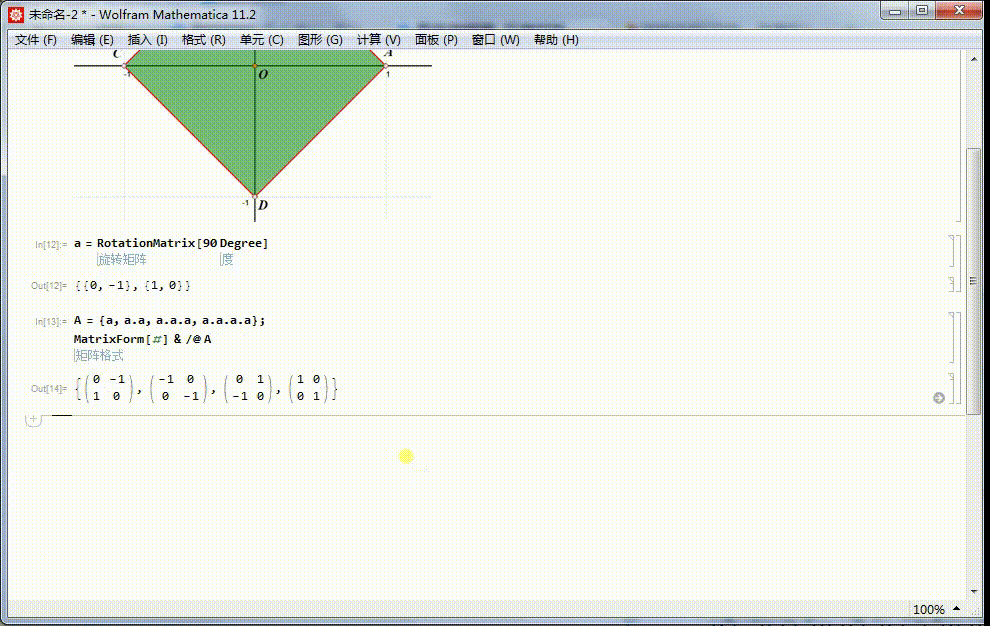
2、a生成一个4阶循环群：{a^0=1,a,a^2,a^3}，相应的矩阵表示是：{I,α,α.α,α.α.α}。这是4阶二面体群的子群。

3、绕x轴的对称变换记为b，保持点的横坐标不变，獭喾酗怛纵坐标变为相反数。相应的矩阵表示记为β。β={{1,1},{1,2}}.Inverse[{{1,1},{-1,-2}}]

4、绕直线y=x的轴对称，记为c，相应的矩阵表示记为γ：γ={{1,1},{1,2}}.Inverse[{{1,2},{1,1}}]

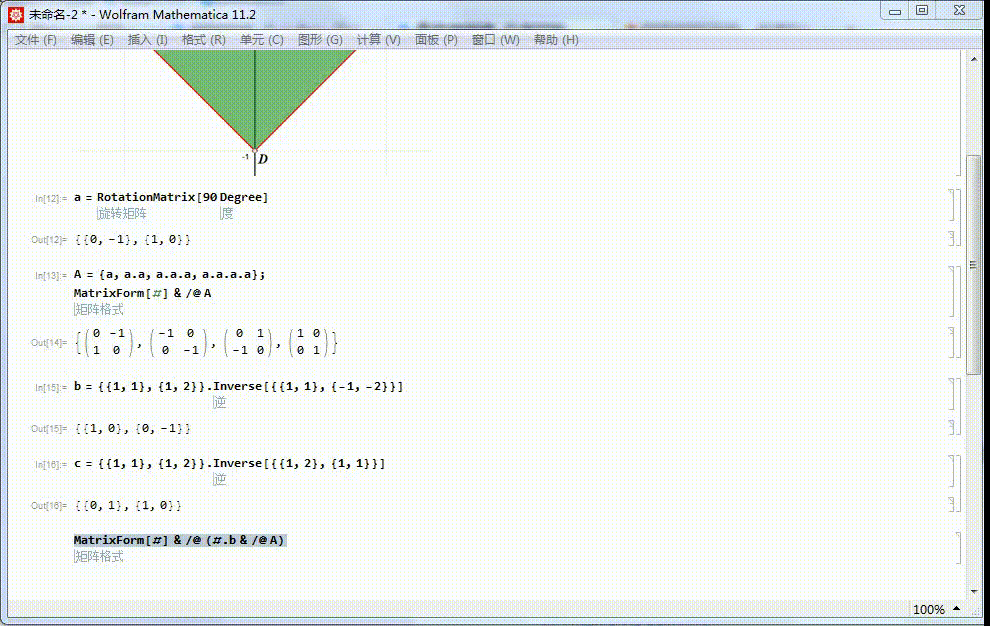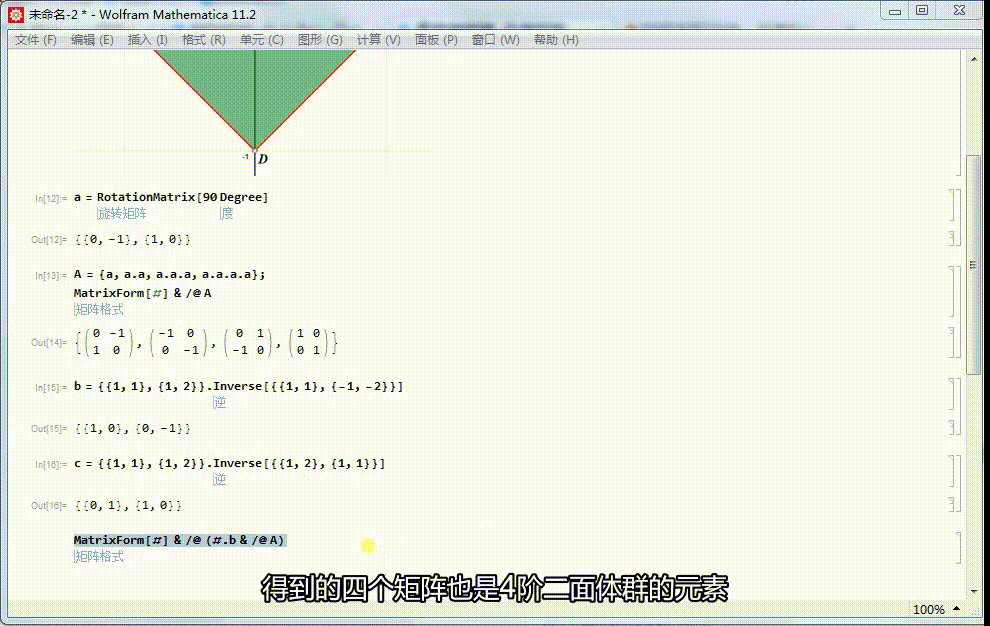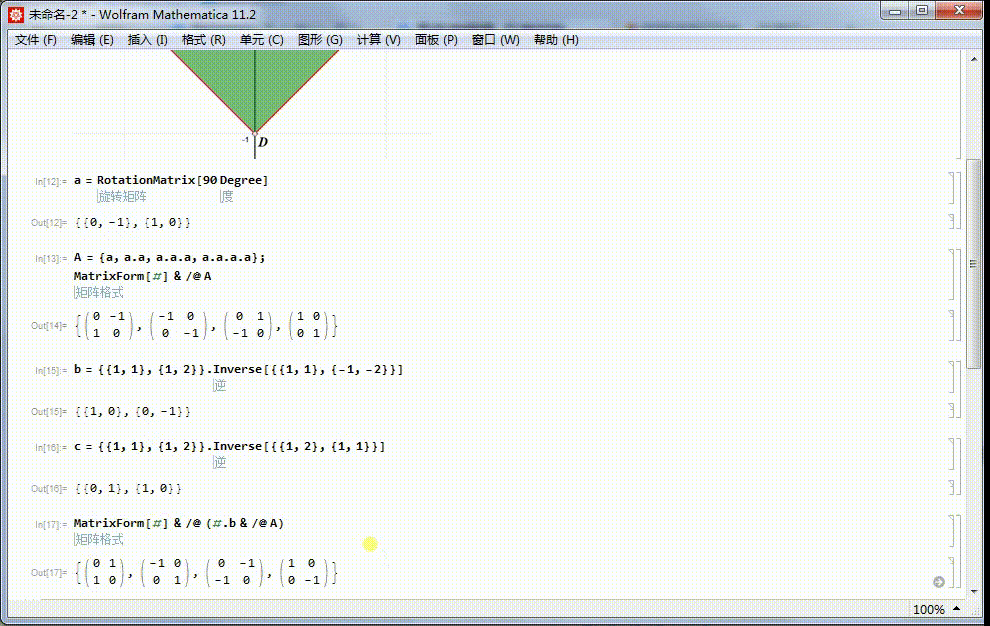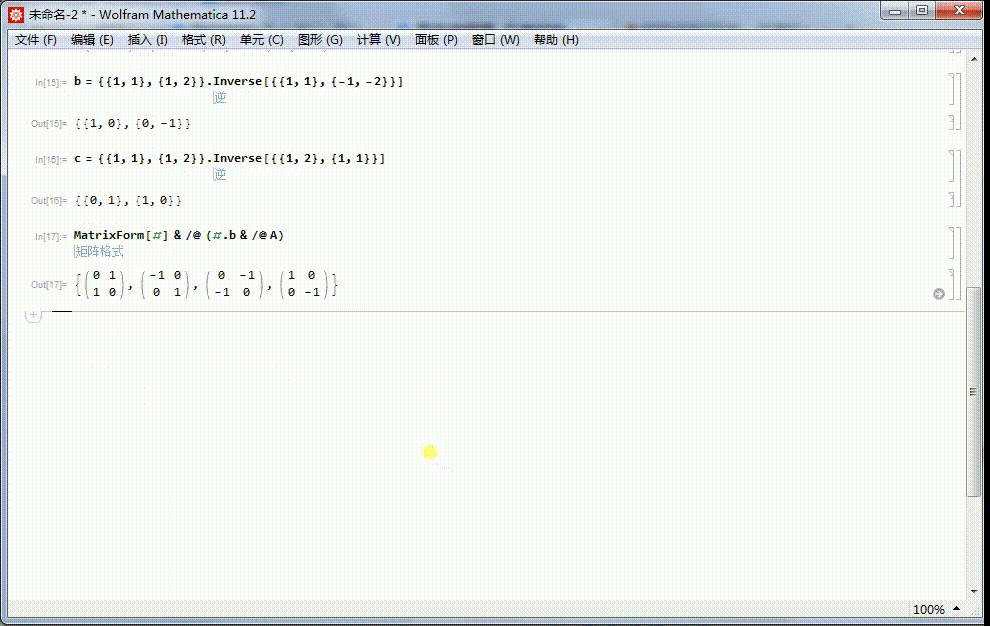
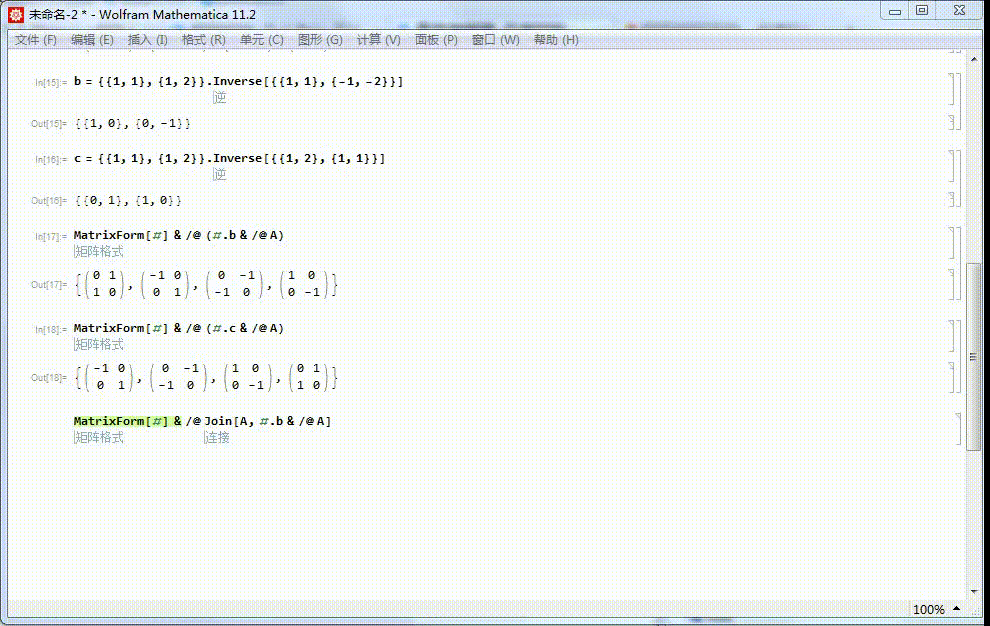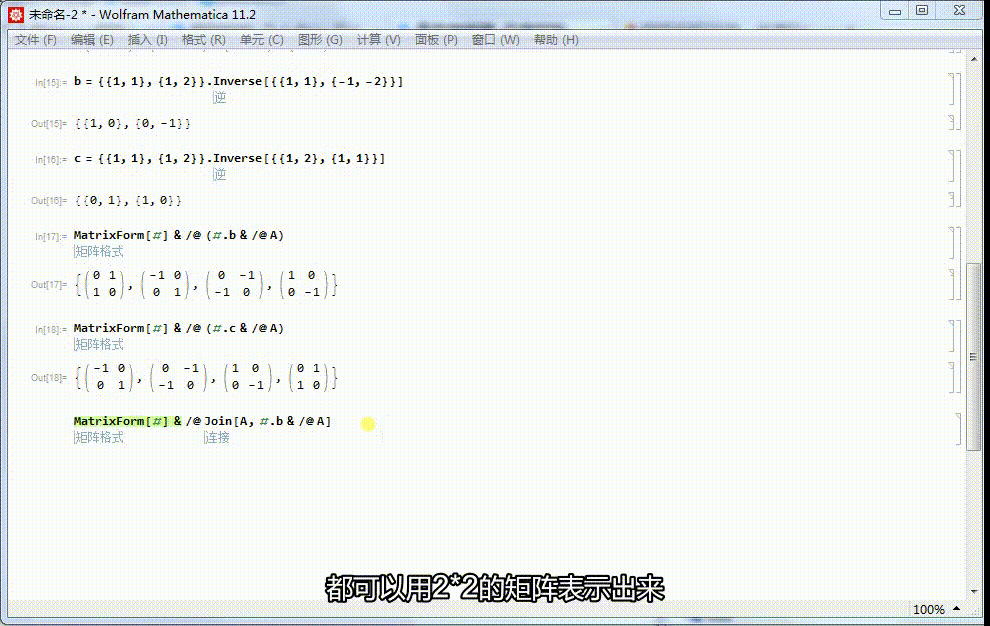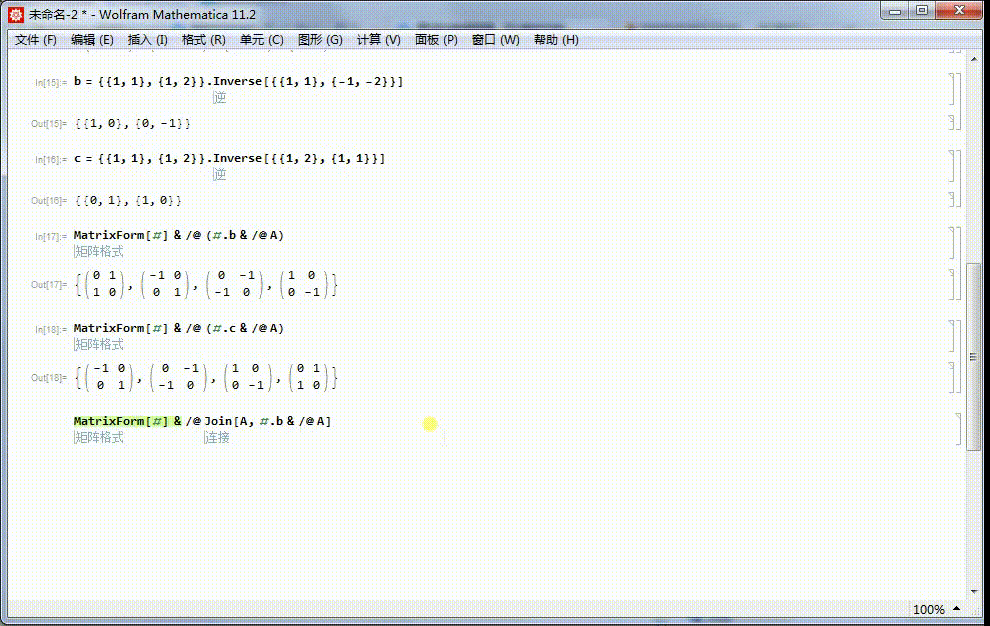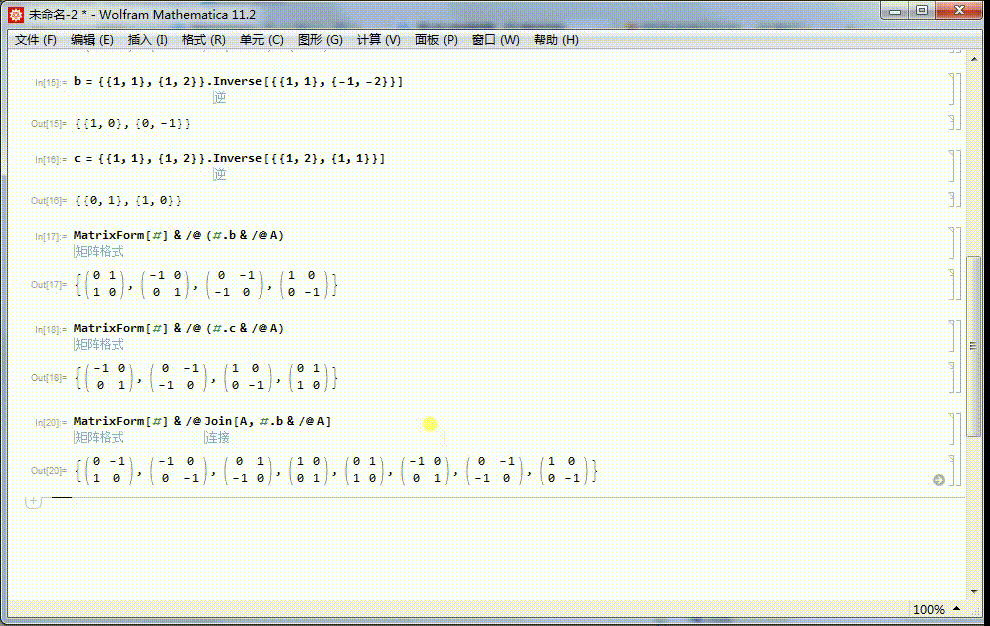
5、由a生成的子群的四个元素，分别和b进行复合，得到的四个矩阵也是4阶二面体群的元素：MatrixForm[#] & /@ (#.b & /@ A)

6、由a生成的子群的四个元素，分别和c进行复合，得到的四个矩阵也是4阶二面体群的元素，而且和上面的结果相同，唯一不同的地方是顺序不同。

7、这样，4阶二面体群的八个元素，都可以用2*2的矩阵表示出来。