函数值域的几种求解方法

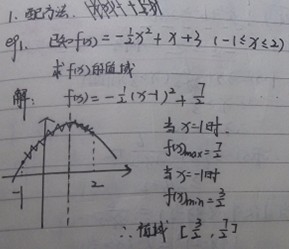
1、一、配方法。将函数配方成顶点式的格式，再根据函数的定义域，求得函数的值域。（画一个简易的图能更便捷直观的求出值域。）

2、二、常数分离这一般是对于分数形式的函数来说的，将分子上的函数尽量配成与分母相同的形式，进行惘度谋裆常数分离，求得值域。

3、三、逆求法对于y=某x的形式，可用逆求法，表示为x=某y，此时可看y的限制范围，就是原式的值域了。

4、四、换元法对于函数的某一部分，较复杂或生疏，可用换元法，将函数转变成我们熟悉的形式，从而求解

5、五、单调性可先求出函数的单调性（注意先求定义域），根据单调性在定义域上求出函数的值域。

6、六、基本不等式根据我们学过的基本不等式，可将函数转换成可运用基本不等式的形式，以此来求值域。

7、七、数形结合可根据函数给出的式子，画出函数的图形，在图形上找出对应点求出值域

8、八、求导法求出函数的导数，观察函数的定义域，将端点值与极值比较，求出最大值与最小值，就可的到值域了。

9、九、判别式法将函数转变成 ****=0 的形式，再用解方程的方法求出要满足的条件，求解即可。