用网络画板演示三角形的均分线

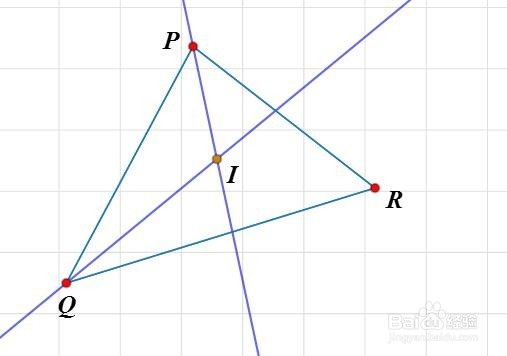
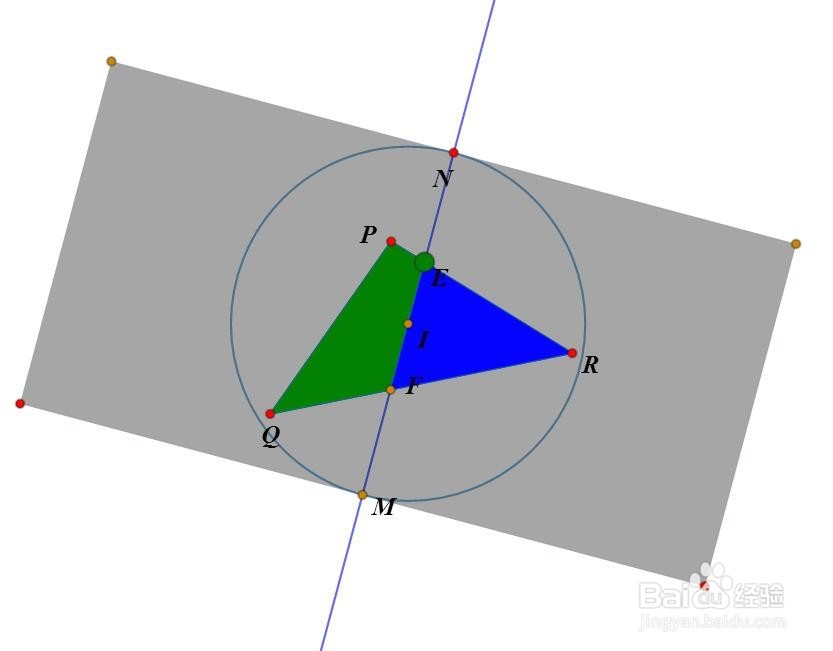
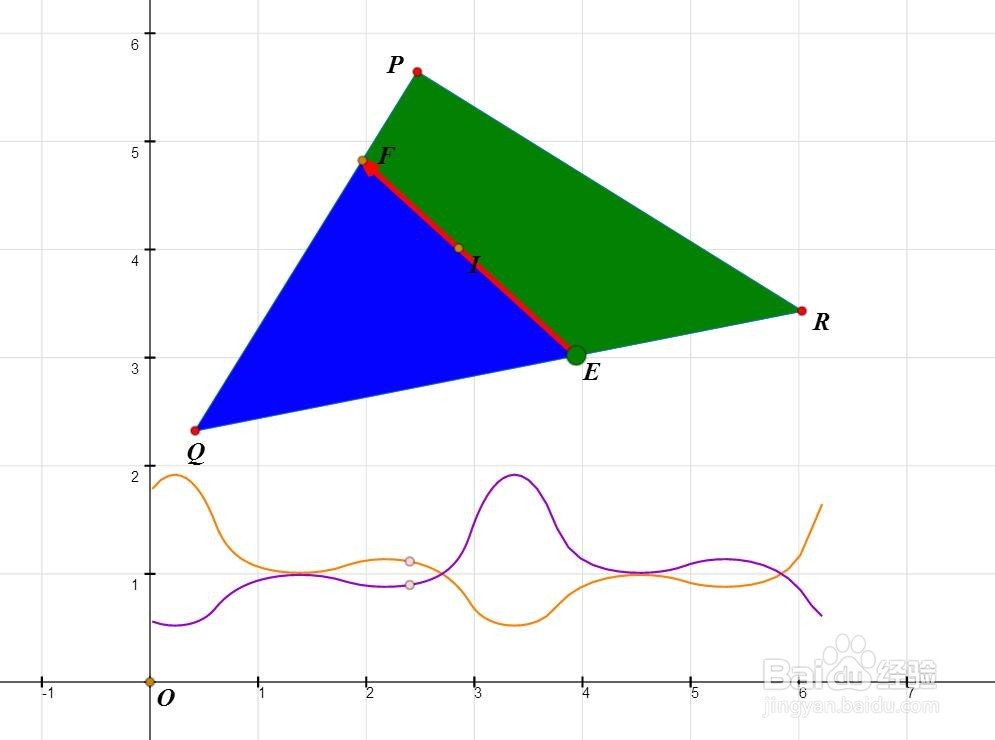
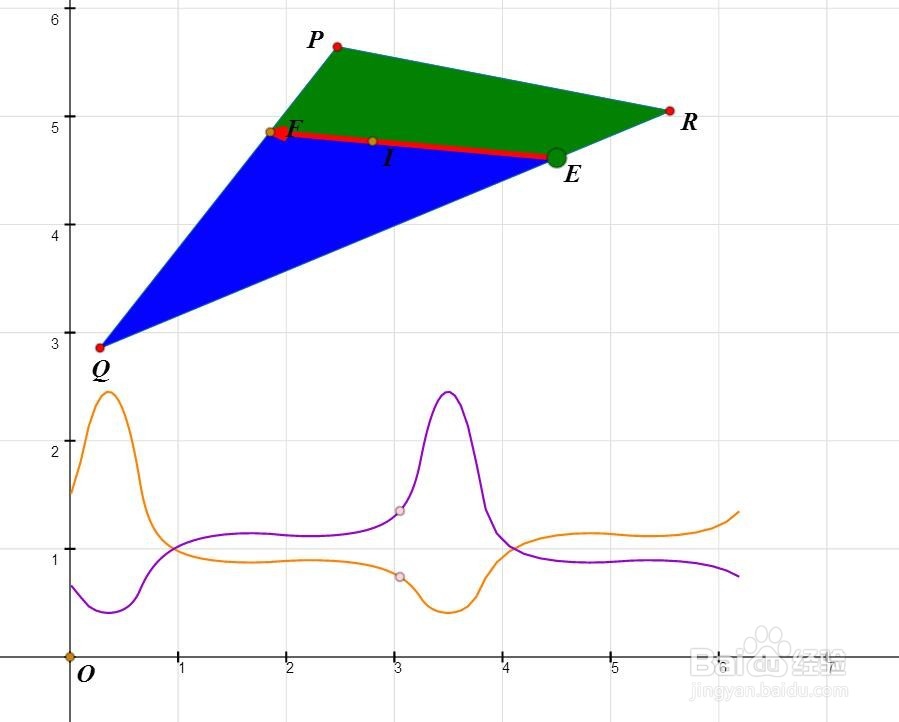
1、理论上可以证明，任意三角形的均分线必定过三角形的内切圆圆心。所以，先作△PQR和内心I。

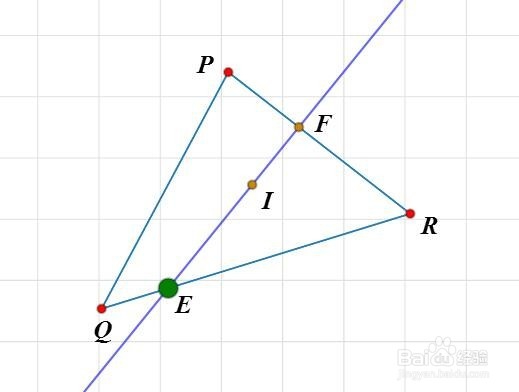
2、E是△PQR边界上的动点，直线EI与△PQR的边界交于另一个点F。

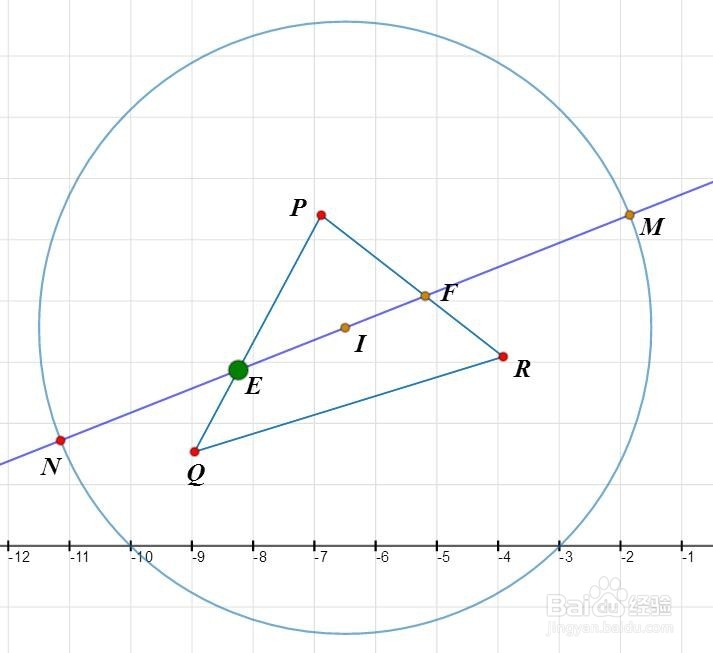
3、以I为圆心作一个圆，此圆可以把△PQR全部盖住；这个圆与直线EF交于M和N。

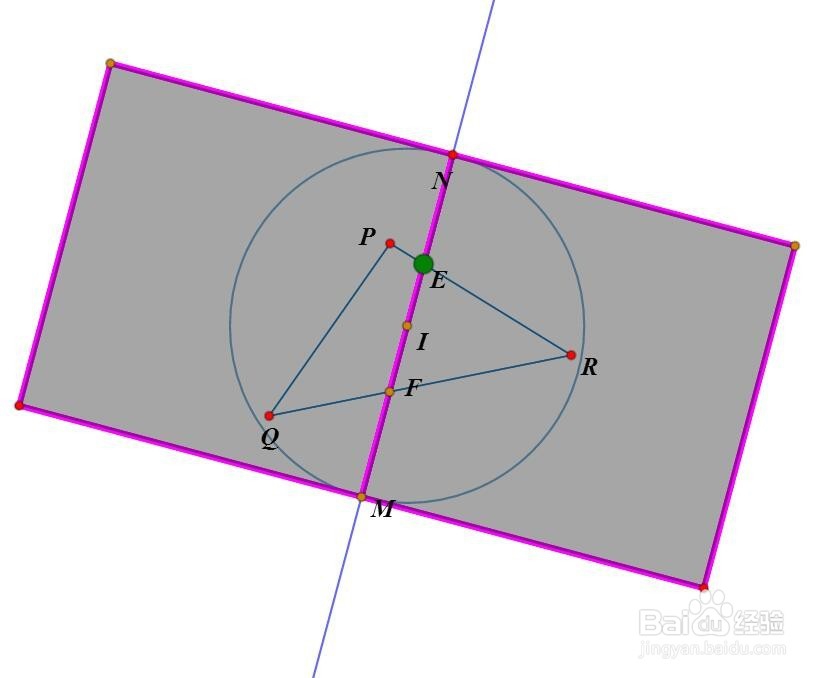
4、以MN为边，分别在向量EF的左右两侧，作正方形。

5、分别作左右两个正方形与△PQR的交，着绿色和蓝色。

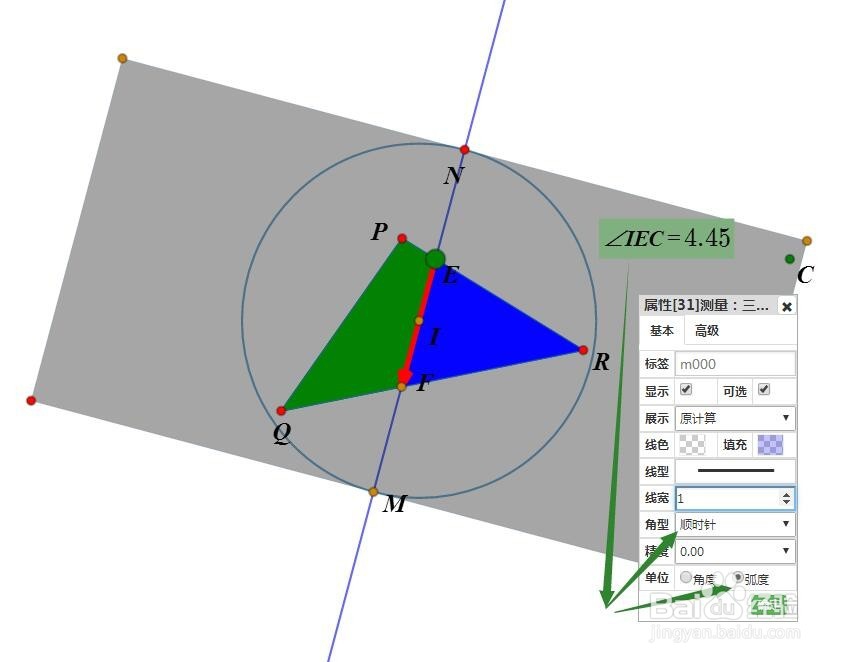
6、E向右平移，得到点C；测量∠IEC的顺时针弧度m000。

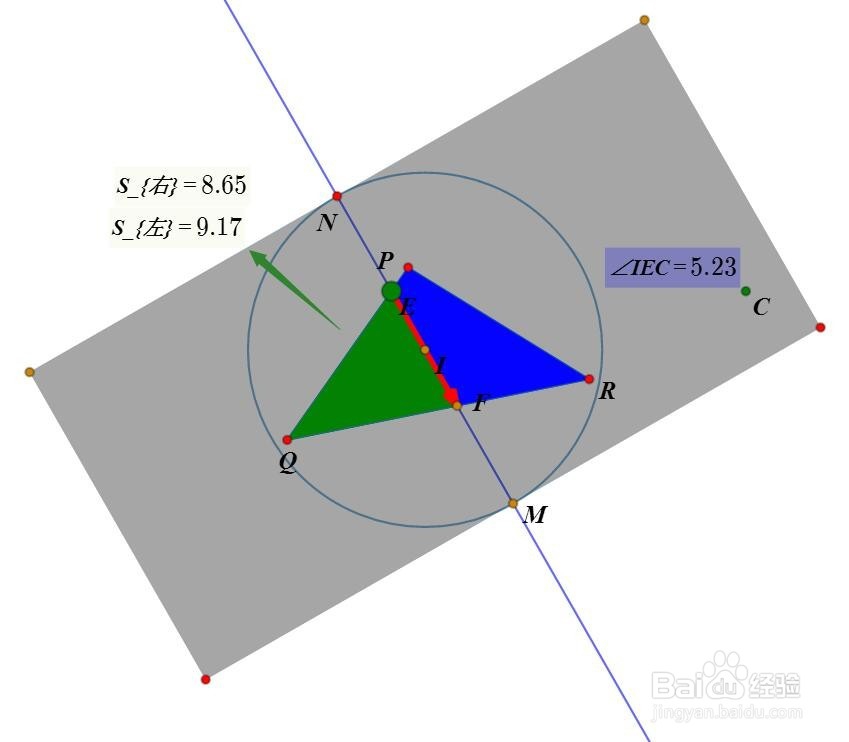
7、分别测量蓝色图形和绿色图形的面积m001和m002。

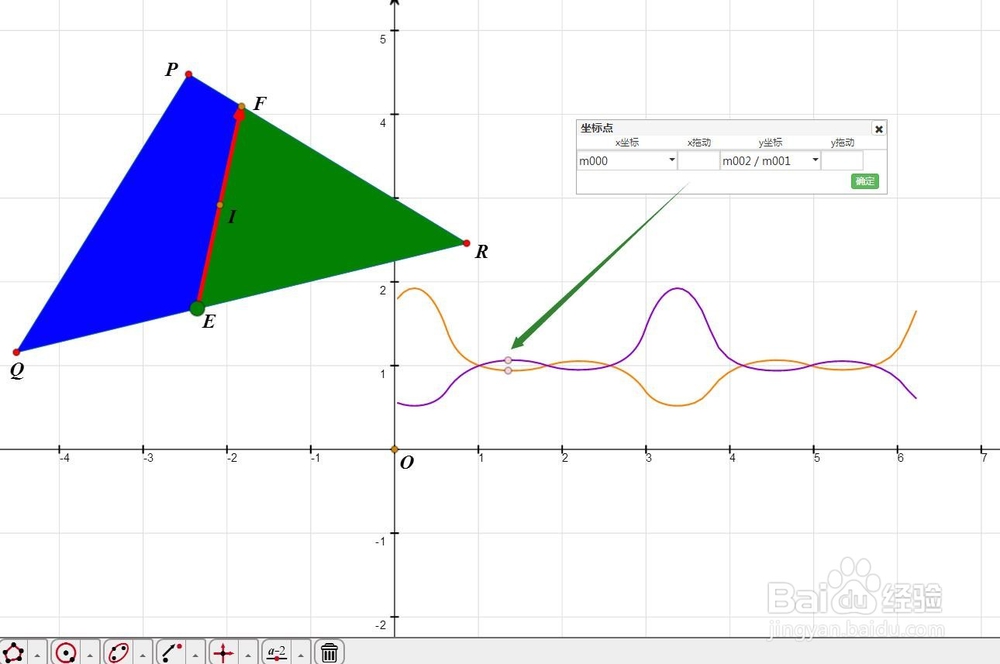
8、分别绘制坐标点（m000，m002/m001）恽但炎杰和（m000，m001/m002）；根据E来构造这两个点的轨迹，如果这两条轨迹有六个交点，那么这个△PQR就有三条均分线。

9、如果轨迹曲线与直线y=1有4个交点，那献垴淄睬么△PQR就只有两条均分线；如果轨迹曲线与直线y=1有2个交点，那么△PQR就只有一条均分线。大家能判断出各种情况下，△PQR的形状吗？