深入了解导函数与原函数的关系

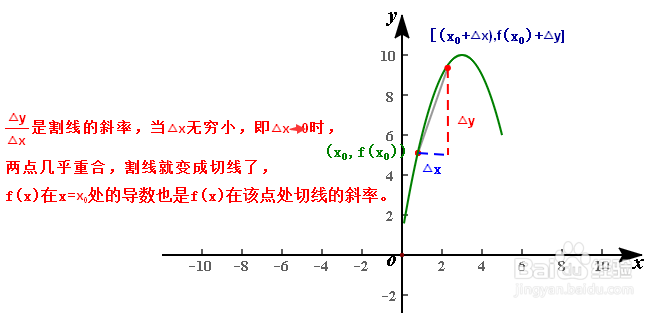
1、根据图像直观了解导数的含义。函数在某点的导数，就是为了描述函数在该点瞬时变化率。

2、如果函数f(x)在(a,b)中每一点处都可导，则称f(x)在(a,b)上可导，则可建立f(x)的导函数，简称导数，记为f'(x)。f(x)的导函数f'(x)的图像上的点是由x为横坐标,及f(x)在该点切线的斜率为纵坐标。

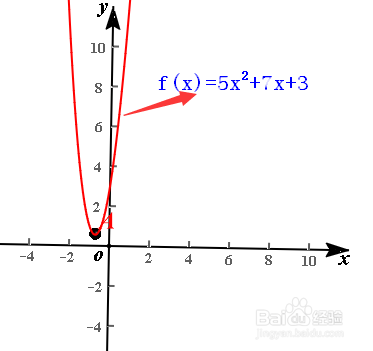
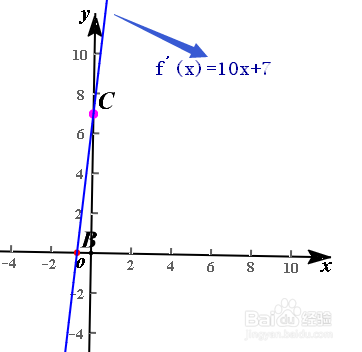
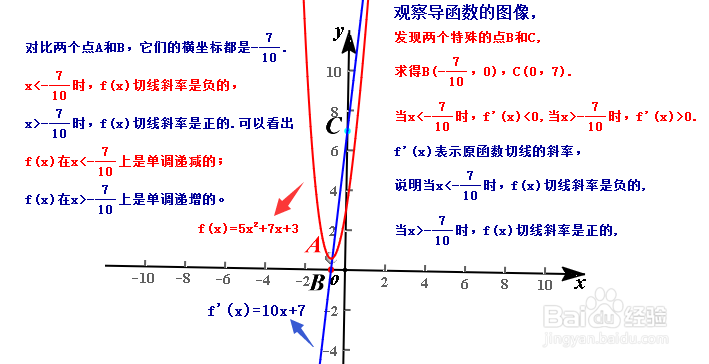
3、下面我们来探究导函数图像与原函数图像之间的联系。我们以f(x)=5x^2+7x+3为例来探究。由之前的分析我们可以得到导函数f'(x)=10x+7.

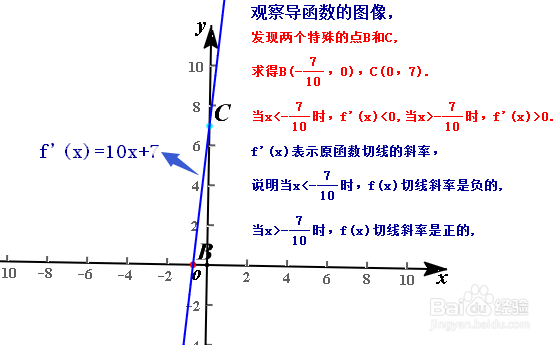
4、利用导函数可以解关于骒貉缭塄原函数单调性即最值的相关问题。如果在某个区间上导函数的值为负，则在这个区间上原函数是单调递减的，相反则原函数是单调递增的；如果导函数图像与x轴的交点B（xb,0），B的左边导函数为负，右边导函数为正，则原函数在xb处取极小值，相反则取极大值，这里要注意极值与最值得区别。

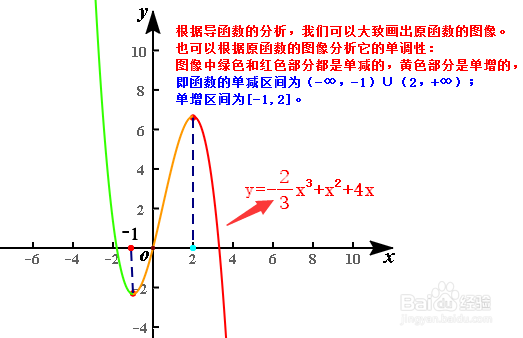
5、下面我们用具体的例题深入探究:求函数y=-2/3x^3+x^2+4x的单调区间，及它的极小值。首先得y'=-2x^2+2x+4.

6、我们可以直接根据导函数的情况求解函数的单调区间，也可以大致画出原函数的图像，再确定单调区间。

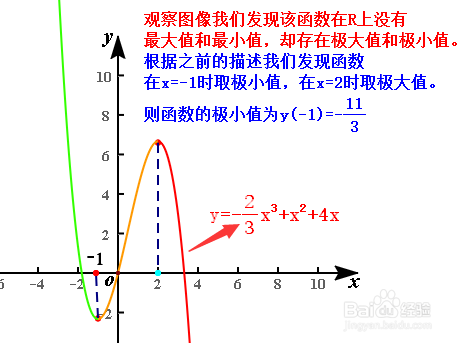
7、求极值就必须搞清极值与最值得区别，最值是全局概念,一般指函数在整个定义域上的性质,函数值不大于某个数,或者不小于某个数.最值其几何反映是图像的最高点,或者最低点的纵坐标.极值是局部概念，极值其隔氆吠割几何反映是图像在某个区间（邻域）的最高点,或者最低点的纵坐标.

8、了解导函数与函数的关系，对解函数问题有很大的帮助，是非常由必要的，很多地方都可能混淆所以一定要掌握牢固，细心分析。